Question Number 164944 by mnjuly1970 last updated on 23/Jan/22
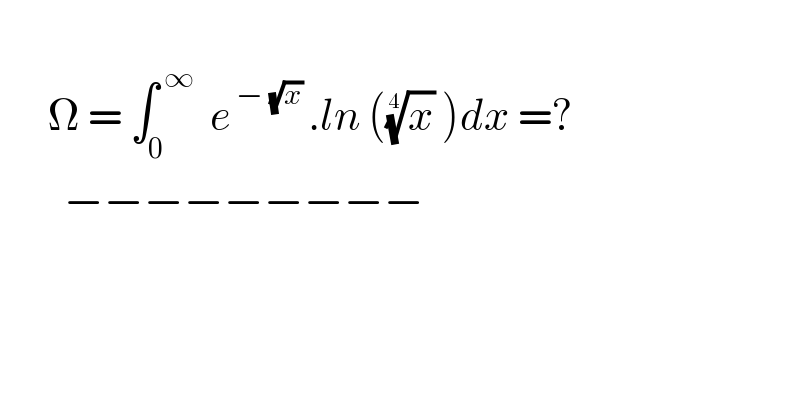
$$ \\ $$$$\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \:\:{e}^{\:−\:\sqrt{{x}}\:} .{ln}\:\left(\sqrt[{\mathrm{4}}]{{x}}\:\right){dx}\:=? \\ $$$$\:\:\:\:\:\:\:\:−−−−−−−−− \\ $$
Answered by Ar Brandon last updated on 24/Jan/22
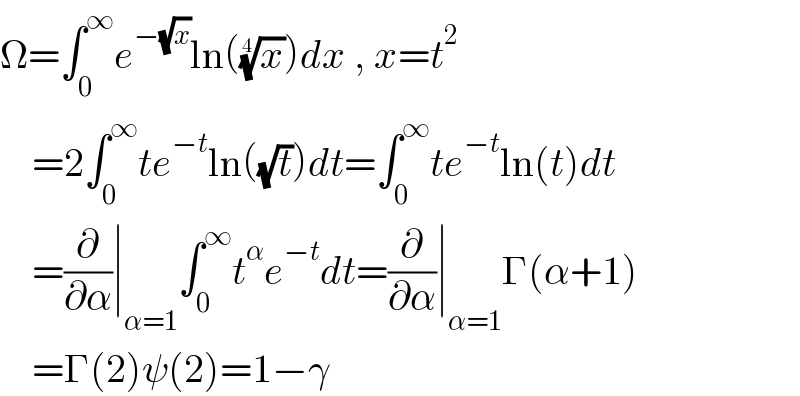
$$\Omega=\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{x}}} \mathrm{ln}\left(\sqrt[{\mathrm{4}}]{{x}}\right){dx}\:,\:{x}={t}^{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {te}^{−{t}} \mathrm{ln}\left(\sqrt{{t}}\right){dt}=\int_{\mathrm{0}} ^{\infty} {te}^{−{t}} \mathrm{ln}\left({t}\right){dt} \\ $$$$\:\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {t}^{\alpha} {e}^{−{t}} {dt}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \Gamma\left(\alpha+\mathrm{1}\right) \\ $$$$\:\:\:\:=\Gamma\left(\mathrm{2}\right)\psi\left(\mathrm{2}\right)=\mathrm{1}−\gamma \\ $$
Commented by mnjuly1970 last updated on 24/Jan/22

$$\:\:\:{thanks}\:{alot}\:{sir}\:{brandon} \\ $$
Commented by Ar Brandon last updated on 24/Jan/22
My pleasure, Sir!
