Question Number 166872 by mnjuly1970 last updated on 01/Mar/22
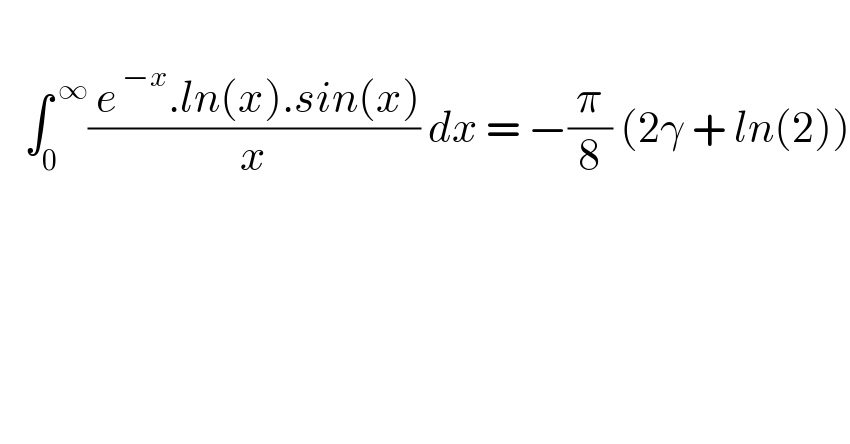
$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{e}^{\:−{x}} .{ln}\left({x}\right).{sin}\left({x}\right)}{{x}}\:{dx}\:=\:−\frac{\pi}{\mathrm{8}}\:\left(\mathrm{2}\gamma\:+\:{ln}\left(\mathrm{2}\right)\right) \\ $$$$ \\ $$
Answered by qaz last updated on 01/Mar/22
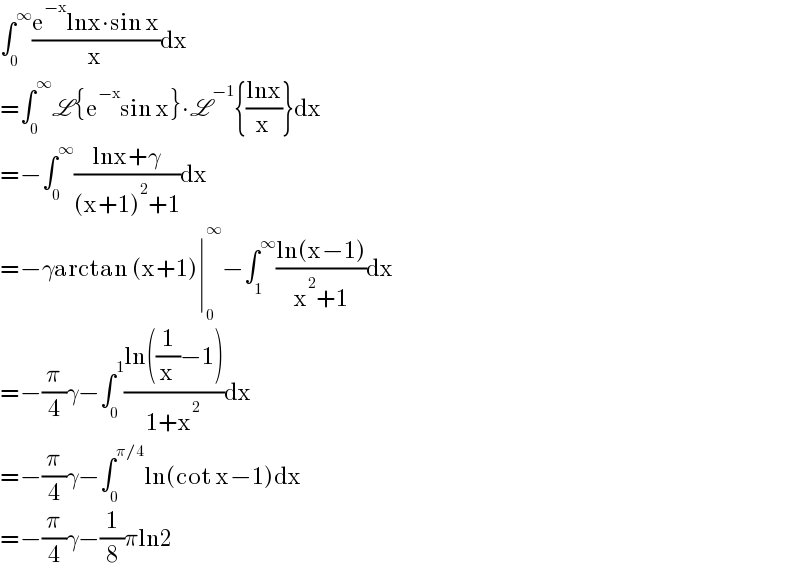
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{x}} \mathrm{lnx}\centerdot\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathscr{L}\left\{\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\mathrm{x}\right\}\centerdot\mathscr{L}^{−\mathrm{1}} \left\{\frac{\mathrm{lnx}}{\mathrm{x}}\right\}\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}+\gamma}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$=−\gamma\mathrm{arctan}\:\left(\mathrm{x}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\infty} −\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\pi}{\mathrm{4}}\gamma−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=−\frac{\pi}{\mathrm{4}}\gamma−\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{ln}\left(\mathrm{cot}\:\mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$=−\frac{\pi}{\mathrm{4}}\gamma−\frac{\mathrm{1}}{\mathrm{8}}\pi\mathrm{ln2} \\ $$
Answered by mindispower last updated on 02/Mar/22
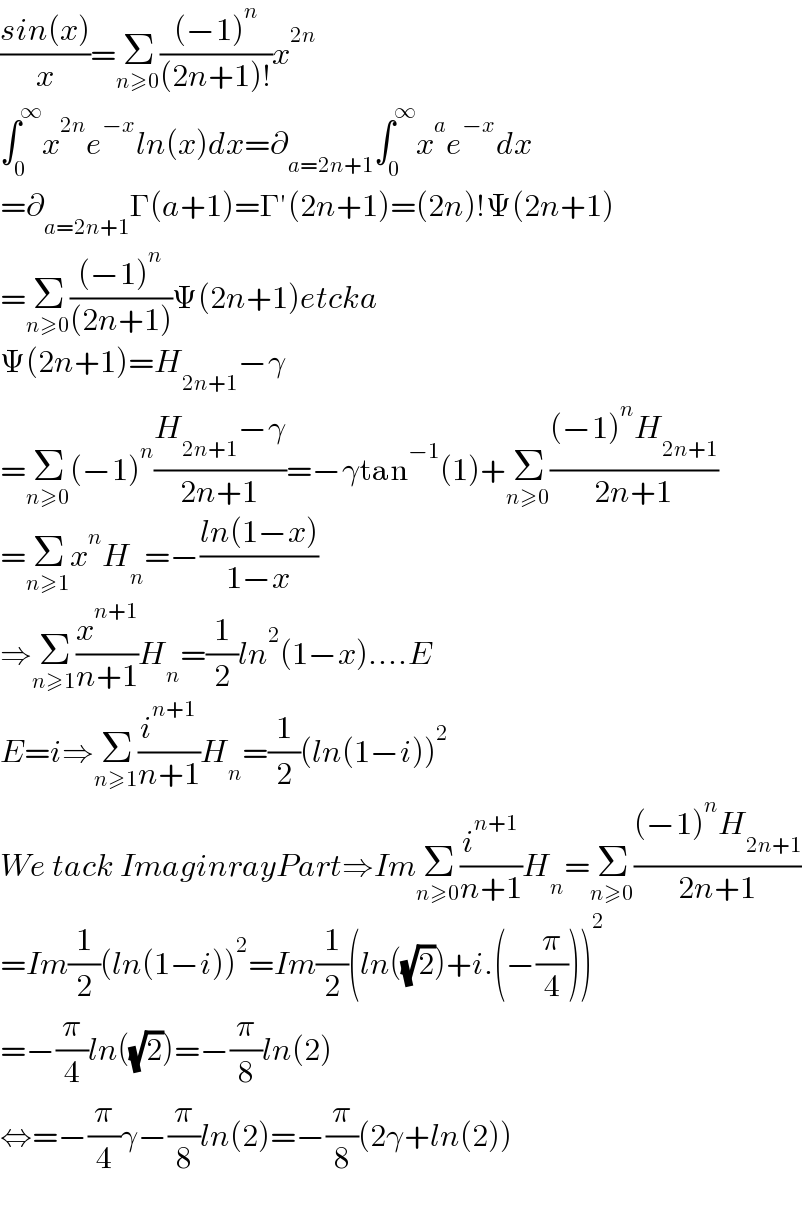
$$\frac{{sin}\left({x}\right)}{{x}}=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{x}^{\mathrm{2}{n}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}{n}} {e}^{−{x}} {ln}\left({x}\right){dx}=\partial_{{a}=\mathrm{2}{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−{x}} {dx} \\ $$$$=\partial_{{a}=\mathrm{2}{n}+\mathrm{1}} \Gamma\left({a}+\mathrm{1}\right)=\Gamma'\left(\mathrm{2}{n}+\mathrm{1}\right)=\left(\mathrm{2}{n}\right)!\Psi\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)}\Psi\left(\mathrm{2}{n}+\mathrm{1}\right){etcka} \\ $$$$\Psi\left(\mathrm{2}{n}+\mathrm{1}\right)={H}_{\mathrm{2}{n}+\mathrm{1}} −\gamma \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{{H}_{\mathrm{2}{n}+\mathrm{1}} −\gamma}{\mathrm{2}{n}+\mathrm{1}}=−\gamma\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}{x}^{{n}} {H}_{{n}} =−\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}} \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{H}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)….{E} \\ $$$${E}={i}\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{i}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{H}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{1}−{i}\right)\right)^{\mathrm{2}} \\ $$$${We}\:{tack}\:{ImaginrayPart}\Rightarrow{Im}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{i}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{H}_{{n}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$={Im}\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{1}−{i}\right)\right)^{\mathrm{2}} ={Im}\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\sqrt{\mathrm{2}}\right)+{i}.\left(−\frac{\pi}{\mathrm{4}}\right)\right)^{\mathrm{2}} \\ $$$$=−\frac{\pi}{\mathrm{4}}{ln}\left(\sqrt{\mathrm{2}}\right)=−\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow=−\frac{\pi}{\mathrm{4}}\gamma−\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)=−\frac{\pi}{\mathrm{8}}\left(\mathrm{2}\gamma+{ln}\left(\mathrm{2}\right)\right) \\ $$$$ \\ $$
