Question Number 182891 by mathlove last updated on 16/Dec/22
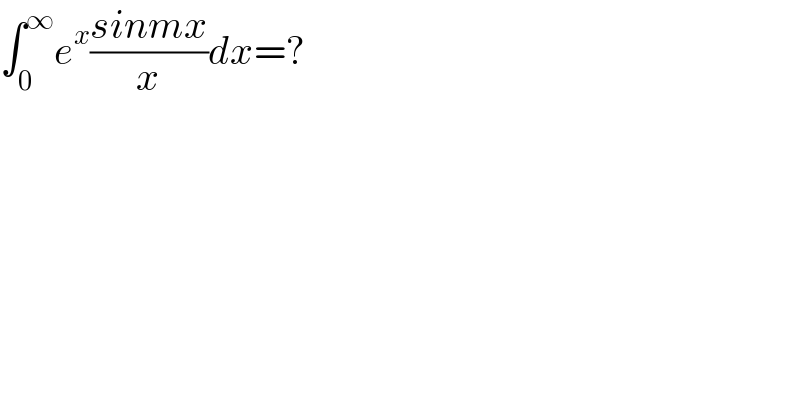
$$\int_{\mathrm{0}\:\:} ^{\infty} {e}^{{x}} \frac{{sinmx}}{{x}}{dx}=? \\ $$
Answered by dre23 last updated on 16/Dec/22
![f(t)=∫_0 ^∞ e^(−x) .((sin(tx))/x)dx f(0)=0 f′(t)=∫_0 ^∞ e^(−x) cos(xt)dx =Re∫_0 ^∞ e^(−(1+it)x) dx,x>0 1+it=(√(1+t^2 ))e^(iarctan(t)) =(√(1+t^2 ))e^(ia(t)) let C=[0,R]∪Re^(iΩ) ,Ω∈[−a(t,)]∪z e^(−ia(t)) ,z∈[0,R]} ∫_C e^(−x) cos(xt)dx=0,∀t>0 holomorphic Function ∫_(Re^(iΩ(t)) ) e^(−x) cos(xt)dx=0 ⇔∫_0 ^∞ e^(−x) cos(xt)dx=Re(1−it)∫_0 ^∞ e^(−(1+it)(1−it)z) dz =Re(1−it)∫_0 ^∞ e^(−(1+t^2 )z) dz.=(1/(1+t^2 )) f′(t)=(1/(1+t^2 ))⇒f(t)=arctan(t)+c f(0)=0⇒f(t)=arctan(t{ ∫_0 ^∞ e^(−x) .((sin(mx))/x)dx=f(m)=arctan(m),∀m≥0](https://www.tinkutara.com/question/Q182901.png)
$${f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} .\frac{{sin}\left({tx}\right)}{{x}}{dx} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {cos}\left({xt}\right){dx} \\ $$$$={Re}\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{1}+{it}\right){x}} {dx},{x}>\mathrm{0} \\ $$$$\mathrm{1}+{it}=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{e}^{{iarctan}\left({t}\right)} =\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{e}^{{ia}\left({t}\right)} \\ $$$$\left.{let}\:{C}=\left[\mathrm{0},{R}\right]\cup{Re}^{{i}\Omega} ,\Omega\in\left[−{a}\left({t},\right)\right]\cup{z}\:{e}^{−{ia}\left({t}\right)} ,{z}\in\left[\mathrm{0},{R}\right]\right\} \\ $$$$\int_{{C}} {e}^{−{x}} {cos}\left({xt}\right){dx}=\mathrm{0},\forall{t}>\mathrm{0}\:{holomorphic}\:{Function} \\ $$$$\int_{{Re}^{{i}\Omega\left({t}\right)} } {e}^{−{x}} {cos}\left({xt}\right){dx}=\mathrm{0} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {cos}\left({xt}\right){dx}={Re}\left(\mathrm{1}−{it}\right)\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{1}+{it}\right)\left(\mathrm{1}−{it}\right){z}} {dz} \\ $$$$={Re}\left(\mathrm{1}−{it}\right)\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{1}+{t}^{\mathrm{2}} \right){z}} {dz}.=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${f}'\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\Rightarrow{f}\left({t}\right)={arctan}\left({t}\right)+{c} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{f}\left({t}\right)={arctan}\left({t}\left\{\right.\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} .\frac{{sin}\left({mx}\right)}{{x}}{dx}={f}\left({m}\right)={arctan}\left({m}\right),\forall{m}\geqslant\mathrm{0} \\ $$$$ \\ $$
Commented by Ml last updated on 16/Dec/22

$$\mathrm{why}\:\mathrm{you}\:\mathrm{e}^{\mathrm{x}} =\mathrm{e}^{−\mathrm{x}} \\ $$
Commented by Peace last updated on 16/Dec/22
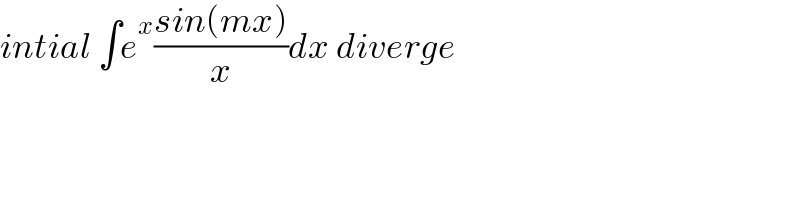
$${intial}\:\int{e}^{{x}} \frac{{sin}\left({mx}\right)}{{x}}{dx}\:{diverge} \\ $$
