Question Number 154823 by talminator2856791 last updated on 21/Sep/21
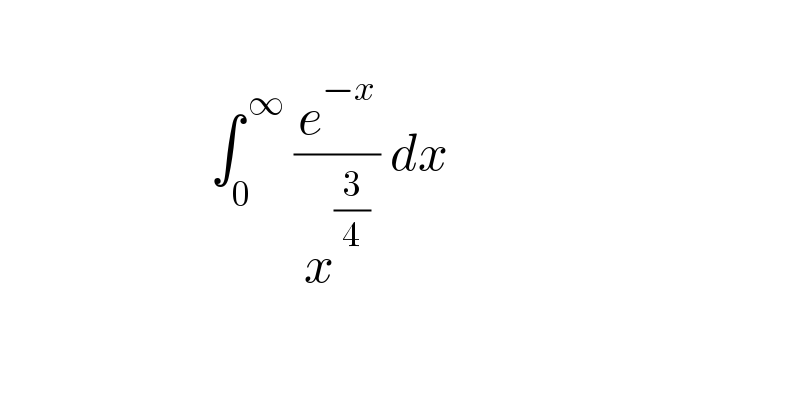
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{e}^{−{x}} }{\:{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \:}\:{dx} \\ $$$$\: \\ $$
Answered by Jonathanwaweh last updated on 21/Sep/21
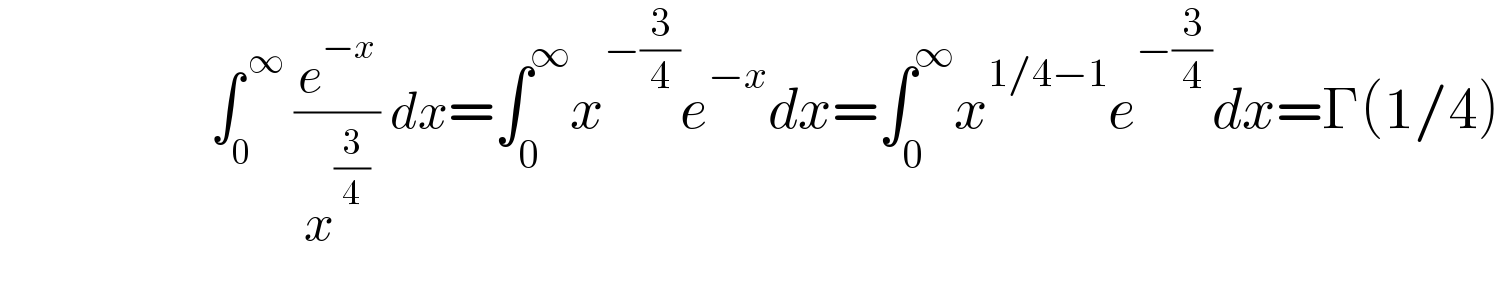
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{e}^{−{x}} }{\:{x}^{\frac{\mathrm{3}}{\mathrm{4}}} \:}\:{dx}=\int_{\mathrm{0}} ^{\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{4}}} {e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}/\mathrm{4}−\mathrm{1}} {e}^{−\frac{\mathrm{3}}{\mathrm{4}}} {dx}=\Gamma\left(\mathrm{1}/\mathrm{4}\right) \\ $$$$ \\ $$
Commented by puissant last updated on 21/Sep/21
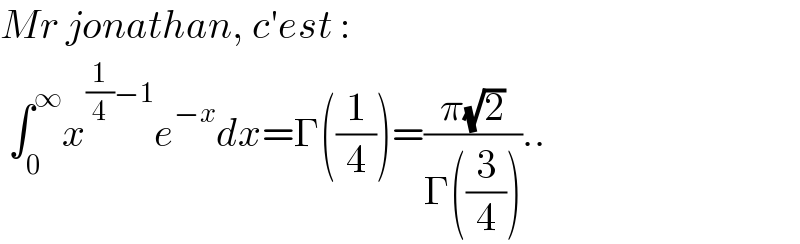
$${Mr}\:{jonathan},\:{c}'{est}\:: \\ $$$$\:\int_{\mathrm{0}} ^{\infty} {x}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {e}^{−{x}} {dx}=\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}.. \\ $$
