Question Number 90192 by Rohit@Thakur last updated on 21/Apr/20
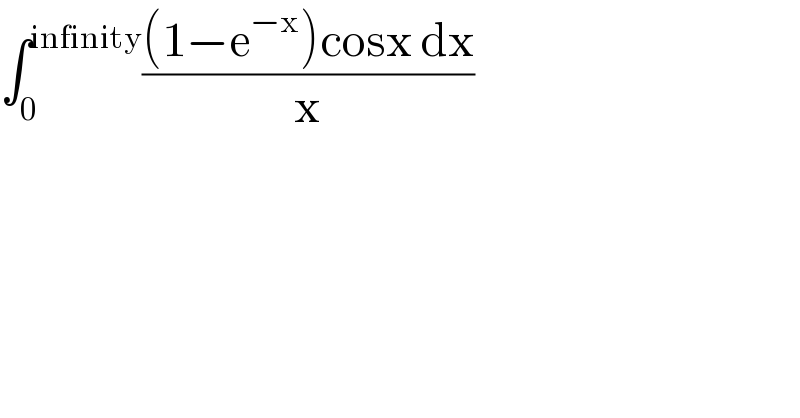
$$\int_{\mathrm{0}} ^{\mathrm{infinity}} \frac{\left(\mathrm{1}−\mathrm{e}^{−\mathrm{x}} \right)\mathrm{cosx}\:\mathrm{dx}}{\mathrm{x}} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
![A =∫_0 ^∞ (((1−e^(−x) )cosx)/x)dx ⇒A =Re(∫_0 ^∞ (((1−e^(−x) )e^(ix) )/x)dx) we have ∫_0 ^∞ ((e^(ix) −e^((−1+i)x) )/x)dx =f(−1+i) with f(a) =∫_0 ^∞ ((e^(ix) −e^(ax) )/x)dx (a from C and Re(a)<0) f^′ (a) =−∫_0 ^∞ e^(ax) dx =−(1/a)[e^(ax) ]_0 ^(+∞) =(1/a) ⇒f(a)=ln(a)+C lim_(a→i) f(a) =0 =ln(i)+C =ln(e^((iπ)/2) ) +C =((iπ)/2) +C ⇒C=−((iπ)/2) f(a) =ln(a)−((iπ)/2) ⇒f(−1+i) =ln(−1+i)−((iπ)/2) =ln((√2)e^(−((iπ)/4)) )−((iπ)/2) =(1/2)ln(2)−((iπ)/4)−((iπ)/2) =((ln(2))/2)−((3iπ)/4) A =Re(∫...) ⇒A =((ln(2))/2)](https://www.tinkutara.com/question/Q90213.png)
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{1}−{e}^{−{x}} \right){cosx}}{{x}}{dx}\:\Rightarrow{A}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{1}−{e}^{−{x}} \right){e}^{{ix}} }{{x}}{dx}\right) \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{{ix}} −{e}^{\left(−\mathrm{1}+{i}\right){x}} }{{x}}{dx}\:={f}\left(−\mathrm{1}+{i}\right)\:{with} \\ $$$${f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{{ix}} −{e}^{{ax}} }{{x}}{dx}\:\:\:\left({a}\:{from}\:{C}\:\:{and}\:{Re}\left({a}\right)<\mathrm{0}\right) \\ $$$${f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:{e}^{{ax}} \:{dx}\:=−\frac{\mathrm{1}}{{a}}\left[{e}^{{ax}} \right]_{\mathrm{0}} ^{+\infty} =\frac{\mathrm{1}}{{a}}\:\Rightarrow{f}\left({a}\right)={ln}\left({a}\right)+{C} \\ $$$${lim}_{{a}\rightarrow{i}} {f}\left({a}\right)\:=\mathrm{0}\:={ln}\left({i}\right)+{C}\:={ln}\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)\:+{C}\:=\frac{{i}\pi}{\mathrm{2}}\:+{C}\:\Rightarrow{C}=−\frac{{i}\pi}{\mathrm{2}} \\ $$$${f}\left({a}\right)\:={ln}\left({a}\right)−\frac{{i}\pi}{\mathrm{2}}\:\Rightarrow{f}\left(−\mathrm{1}+{i}\right)\:={ln}\left(−\mathrm{1}+{i}\right)−\frac{{i}\pi}{\mathrm{2}} \\ $$$$={ln}\left(\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)−\frac{{i}\pi}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{{i}\pi}{\mathrm{4}}−\frac{{i}\pi}{\mathrm{2}}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\mathrm{3}{i}\pi}{\mathrm{4}} \\ $$$${A}\:={Re}\left(\int…\right)\:\Rightarrow{A}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA. last updated on 21/Apr/20
![another approach... ∫_0 ^∞ e^(−ax) cosbx dx=(a/(a^2 +b^2 )) ∫_0 ^∞ [∫_α ^β e^(−ax) da] cosbx dx=∫_α ^β (a/(a^2 +b^2 ))da ∫_0 ^∞ ∣(e^(−ax) /(−x))∣_α ^β cosbx dx=(1/2)∫_α ^β ((d(a^2 +b^2 ))/(a^2 +b^2 )) ∫_0 ^∞ (((e^(−αx) −e^(−βx) )/x))cosbx dx=(1/2)∣ln(a^2 +b^2 )∣_α ^β ∫_0 ^∞ (((e^(−αx) −e^(−βx) )/x))cosbx=(1/2)ln(((β^2 +b^2 )/(α^2 +b^2 ))) now put α=0 β=1 b=1 ∫_0 ^∞ (((1−e^(−x) )/x))cosx dx=(1/2)ln(((1+1)/(0+1)))=(1/2)ln2 solved using ML khanna book formula](https://www.tinkutara.com/question/Q90199.png)
$${another}\:{approach}… \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {cosbx}\:{dx}=\frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \left[\int_{\alpha} ^{\beta} {e}^{−{ax}} {da}\right]\:{cosbx}\:{dx}=\int_{\alpha} ^{\beta} \frac{{a}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{da} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mid\frac{{e}^{−{ax}} }{−{x}}\mid_{\alpha} ^{\beta} {cosbx}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\alpha} ^{\beta} \frac{{d}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−\alpha{x}} −{e}^{−\beta{x}} }{{x}}\right){cosbx}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mid{ln}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\mid_{\alpha} ^{\beta} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−\alpha{x}} −{e}^{−\beta{x}} }{{x}}\right){cosbx}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\beta^{\mathrm{2}} +{b}^{\mathrm{2}} }{\alpha^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$${now}\:{put}\:\alpha=\mathrm{0}\:\:\:\beta=\mathrm{1}\:\:{b}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}−{e}^{−{x}} }{{x}}\right){cosx}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+\mathrm{1}}{\mathrm{0}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2} \\ $$$${solved}\:{using}\:{ML}\:{khanna}\:{book}\:{formula} \\ $$
