Menu Close

0-ln-1-a-2-x-2-1-b-2-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 150841 by mathdanisur last updated on 15/Aug/21
∫_( 0) ^( ∞) ((ln(1+a^2 x^2 ))/(1+b^2 x^2 )) dx = ?
$$\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{b}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 15/Aug/21
f(a,b) = ∫_0 ^∞ ((ln(1+a^2 x^2 ))/(1+b^2 x^2 )) dx (1) (∂f/∂a)(a,b) = ∫_0 ^∞ ((2ax^2 )/((1+a^2 x^2 )(1+b^2 x^2 ))) dx (∂f/∂a)(a,b) = ((2a)/(b^2 −a^2 ))∫_0 ^∞ ((1/(1+a^2 x^2 ))−(1/(1+b^2 x^2 ))) dx (∂f/∂a)(a,b) = ((2a)/(b^2 −a^2 ))[((arctan(ax))/a)−((arctan(bx))/b)]_0 ^∞ (∂f/∂a)(a,b) = ((2a)/(b^2 −a^2 ))((π/(2a))−(π/(2b))) (∂f/∂a)(a,b) = (π/(b(a+b))) ⇒ f(a,b) = (π/b)ln(a+b)+C(b) (2) (1) : f(0,b) = ∫_0 ^∞ ((ln(1+0x^2 ))/(1+b^2 x^2 )) dx = 0 (2) : f(0,b) = (π/b)ln(0+b)+C(b) = (π/b)lnb+C(b) ⇒ C(b) = −(π/b)lnb (2) : f(a,b) = (π/b)ln(a+b)−(π/b)lnb f(a,b) = (π/b)ln(1+(a/b))
$${f}\left({a},{b}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{\mathrm{1}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} }\:{dx}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\frac{\partial{f}}{\partial{a}}\left({a},{b}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{ax}^{\mathrm{2}} }{\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:{dx} \\ $$$$\frac{\partial{f}}{\partial{a}}\left({a},{b}\right)\:=\:\frac{\mathrm{2}{a}}{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} }\right)\:{dx} \\ $$$$\frac{\partial{f}}{\partial{a}}\left({a},{b}\right)\:=\:\frac{\mathrm{2}{a}}{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\left[\frac{\mathrm{arctan}\left({ax}\right)}{{a}}−\frac{\mathrm{arctan}\left({bx}\right)}{{b}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\frac{\partial{f}}{\partial{a}}\left({a},{b}\right)\:=\:\frac{\mathrm{2}{a}}{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\left(\frac{\pi}{\mathrm{2}{a}}−\frac{\pi}{\mathrm{2}{b}}\right) \\ $$$$\frac{\partial{f}}{\partial{a}}\left({a},{b}\right)\:=\:\frac{\pi}{{b}\left({a}+{b}\right)} \\ $$$$\Rightarrow\:{f}\left({a},{b}\right)\:=\:\frac{\pi}{{b}}\mathrm{ln}\left({a}+{b}\right)+\mathrm{C}\left({b}\right)\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\::\:{f}\left(\mathrm{0},{b}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{0}{x}^{\mathrm{2}} \right)}{\mathrm{1}+{b}^{\mathrm{2}} {x}^{\mathrm{2}} }\:{dx}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\::\:{f}\left(\mathrm{0},{b}\right)\:=\:\frac{\pi}{{b}}\mathrm{ln}\left(\mathrm{0}+{b}\right)+\mathrm{C}\left({b}\right)\:=\:\:\frac{\pi}{{b}}\mathrm{ln}{b}+\mathrm{C}\left({b}\right) \\ $$$$\Rightarrow\:\mathrm{C}\left({b}\right)\:=\:−\frac{\pi}{{b}}\mathrm{ln}{b} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\::\:{f}\left({a},{b}\right)\:=\:\frac{\pi}{{b}}\mathrm{ln}\left({a}+{b}\right)−\frac{\pi}{{b}}\mathrm{ln}{b} \\ $$$$ \\ $$$${f}\left({a},{b}\right)\:=\:\frac{\pi}{{b}}\mathrm{ln}\left(\mathrm{1}+\frac{{a}}{{b}}\right) \\ $$
Commented by amin96 last updated on 15/Aug/21
nice
$${nice} \\ $$
Commented by mathdanisur last updated on 15/Aug/21
Thank you Ser cool
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser}\:\mathrm{cool} \\ $$
Answered by mathmax by abdo last updated on 17/Aug/21
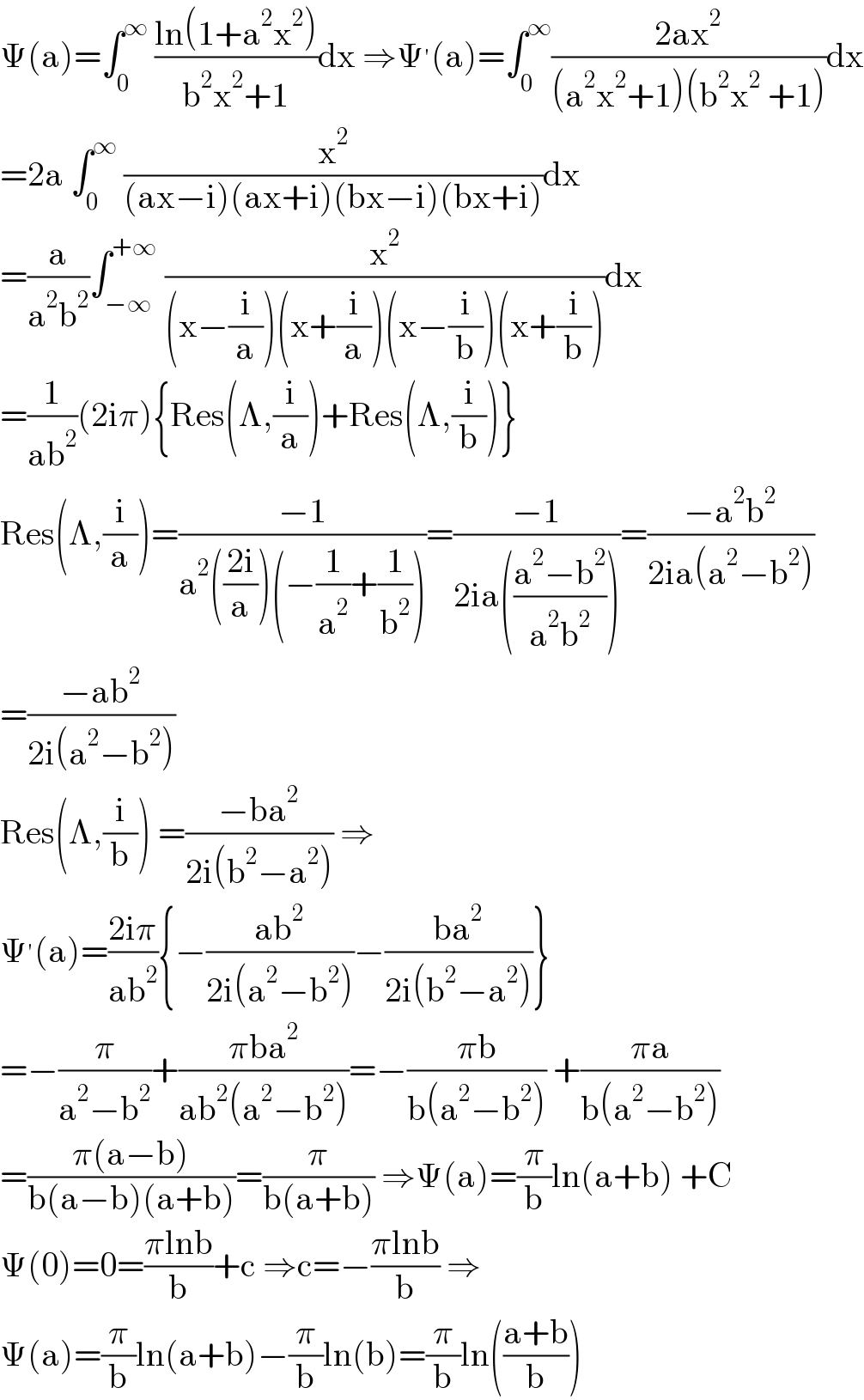
Ψ(a)=∫_0 ^∞ ((ln(1+a^2 x^2 ))/(b^2 x^2 +1))dx ⇒Ψ^′ (a)=∫_0 ^∞ ((2ax^2 )/((a^2 x^2 +1)(b^2 x^2 +1)))dx =2a ∫_0 ^∞ (x^2 /((ax−i)(ax+i)(bx−i)(bx+i)))dx =(a/(a^2 b^2 ))∫_(−∞) ^(+∞) (x^2 /((x−(i/a))(x+(i/a))(x−(i/b))(x+(i/b))))dx =(1/(ab^2 ))(2iπ){Res(Λ,(i/a))+Res(Λ,(i/b))} Res(Λ,(i/a))=((−1)/(a^2 (((2i)/a))(−(1/a^2 )+(1/b^2 ))))=((−1)/(2ia(((a^2 −b^2 )/(a^2 b^2 )))))=((−a^2 b^2 )/(2ia(a^2 −b^2 ))) =((−ab^2 )/(2i(a^2 −b^2 ))) Res(Λ,(i/b)) =((−ba^2 )/(2i(b^2 −a^2 ))) ⇒ Ψ^′ (a)=((2iπ)/(ab^2 )){−((ab^2 )/(2i(a^2 −b^2 )))−((ba^2 )/(2i(b^2 −a^2 )))} =−(π/(a^2 −b^2 ))+((πba^2 )/(ab^2 (a^2 −b^2 )))=−((πb)/(b(a^2 −b^2 ))) +((πa)/(b(a^2 −b^2 ))) =((π(a−b))/(b(a−b)(a+b)))=(π/(b(a+b))) ⇒Ψ(a)=(π/b)ln(a+b) +C Ψ(0)=0=((πlnb)/b)+c ⇒c=−((πlnb)/b) ⇒ Ψ(a)=(π/b)ln(a+b)−(π/b)ln(b)=(π/b)ln(((a+b)/b))
$$\Psi\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)}{\mathrm{b}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:\Rightarrow\Psi^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2ax}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{b}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\mathrm{2a}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{ax}−\mathrm{i}\right)\left(\mathrm{ax}+\mathrm{i}\right)\left(\mathrm{bx}−\mathrm{i}\right)\left(\mathrm{bx}+\mathrm{i}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}−\frac{\mathrm{i}}{\mathrm{a}}\right)\left(\mathrm{x}+\frac{\mathrm{i}}{\mathrm{a}}\right)\left(\mathrm{x}−\frac{\mathrm{i}}{\mathrm{b}}\right)\left(\mathrm{x}+\frac{\mathrm{i}}{\mathrm{b}}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{ab}^{\mathrm{2}} }\left(\mathrm{2i}\pi\right)\left\{\mathrm{Res}\left(\Lambda,\frac{\mathrm{i}}{\mathrm{a}}\right)+\mathrm{Res}\left(\Lambda,\frac{\mathrm{i}}{\mathrm{b}}\right)\right\} \\ $$$$\mathrm{Res}\left(\Lambda,\frac{\mathrm{i}}{\mathrm{a}}\right)=\frac{−\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \left(\frac{\mathrm{2i}}{\mathrm{a}}\right)\left(−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} }\right)}=\frac{−\mathrm{1}}{\mathrm{2ia}\left(\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }\right)}=\frac{−\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }{\mathrm{2ia}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{−\mathrm{ab}^{\mathrm{2}} }{\mathrm{2i}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{Res}\left(\Lambda,\frac{\mathrm{i}}{\mathrm{b}}\right)\:=\frac{−\mathrm{ba}^{\mathrm{2}} }{\mathrm{2i}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\Psi^{'} \left(\mathrm{a}\right)=\frac{\mathrm{2i}\pi}{\mathrm{ab}^{\mathrm{2}} }\left\{−\frac{\mathrm{ab}^{\mathrm{2}} }{\mathrm{2i}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}−\frac{\mathrm{ba}^{\mathrm{2}} }{\mathrm{2i}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}\right\} \\ $$$$=−\frac{\pi}{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }+\frac{\pi\mathrm{ba}^{\mathrm{2}} }{\mathrm{ab}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}=−\frac{\pi\mathrm{b}}{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}\:+\frac{\pi\mathrm{a}}{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi\left(\mathrm{a}−\mathrm{b}\right)}{\mathrm{b}\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{a}+\mathrm{b}\right)}=\frac{\pi}{\mathrm{b}\left(\mathrm{a}+\mathrm{b}\right)}\:\Rightarrow\Psi\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{b}}\mathrm{ln}\left(\mathrm{a}+\mathrm{b}\right)\:+\mathrm{C} \\ $$$$\Psi\left(\mathrm{0}\right)=\mathrm{0}=\frac{\pi\mathrm{lnb}}{\mathrm{b}}+\mathrm{c}\:\Rightarrow\mathrm{c}=−\frac{\pi\mathrm{lnb}}{\mathrm{b}}\:\Rightarrow \\ $$$$\Psi\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{b}}\mathrm{ln}\left(\mathrm{a}+\mathrm{b}\right)−\frac{\pi}{\mathrm{b}}\mathrm{ln}\left(\mathrm{b}\right)=\frac{\pi}{\mathrm{b}}\mathrm{ln}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{b}}\right) \\ $$
Commented by mathdanisur last updated on 18/Aug/21
Thank you Ser
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *