Question Number 28006 by sorour87 last updated on 18/Jan/18
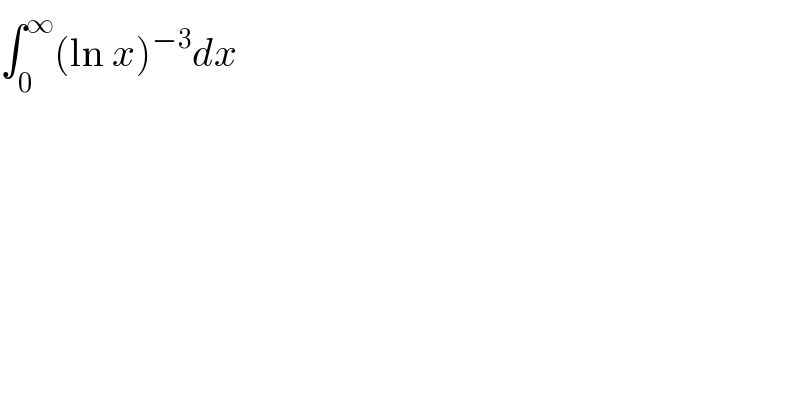
$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{ln}\:{x}\right)^{−\mathrm{3}} {dx} \\ $$
Commented by abdo imad last updated on 20/Jan/18

$${the}\:{ch}\:.{lnx}={t}\:{give}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\left({lnx}\right)^{−\mathrm{3}} {dx}=\:\int_{−\infty} ^{+\infty} \:\:{t}^{−\mathrm{3}} \:{e}^{{t}} {dt} \\ $$$$=\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}=\:\int_{−\infty} ^{\mathrm{0}} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:+\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\:\int_{−\infty} ^{−\mathrm{1}} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:+\int_{−\mathrm{1}} ^{\mathrm{0}\:\:\:} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:++\left(…\right)\:+\left(…\right)\:{but} \\ $$$$\:\int_{−\infty} ^{−\mathrm{1}} \:\:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:=\:−\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{−{x}} }{{x}^{\mathrm{3}} }{dx}\:\:\:{and}\:{this}\:{integral}\:{converges}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}=−{x} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{e}^{−{x}} }{{x}^{\mathrm{3}} }{dx}\:\:{this}\:{integral}\:{diverges} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{{t}} }{{t}^{\mathrm{3}} }{dt}\:{converges}\:{so}\:{the}\:{integral}\:\int_{\mathrm{0}} ^{\infty} \left({lnx}\right)^{−\mathrm{3}} {dx}\:{diverges} \\ $$
