Question Number 155207 by mathdanisur last updated on 26/Sep/21
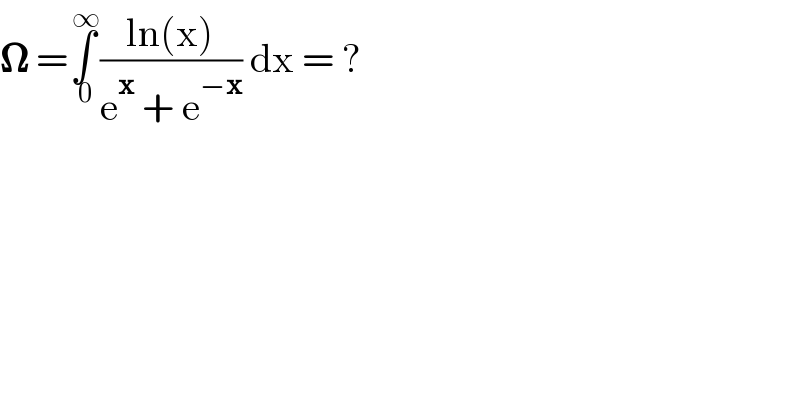
$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{e}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{e}^{−\boldsymbol{\mathrm{x}}} }\:\mathrm{dx}\:=\:? \\ $$
Answered by mindispower last updated on 27/Sep/21

$$\Omega={f}'\left(\mathrm{0}\right),{f}'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} }{{e}^{{x}} +{e}^{−{x}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{a}} \underset{{k}} {\sum}\left(−\mathrm{1}\right)^{{k}} {e}^{−\left(\mathrm{1}+\mathrm{2}{k}\right){x}} {dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} {e}^{−{x}} }{\left(\mathrm{1}+\mathrm{2}{k}\right)^{{a}+\mathrm{1}} }{dx}=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} \frac{\Gamma\left(\mathrm{1}+{a}\right)}{\left(\mathrm{1}+\mathrm{2}{k}\right)^{{a}+\mathrm{1}} } \\ $$$$=\frac{\Gamma\left(\mathrm{1}+{a}\right)}{\mathrm{2}^{\mathrm{1}+{a}} }\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{{a}+\mathrm{1}} }−\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{{a}+\mathrm{1}} } \\ $$$$=\frac{\Gamma\left(\mathrm{1}+{a}\right)}{\mathrm{2}^{\mathrm{1}+{a}} }\left(\zeta\left(\frac{\mathrm{1}}{\mathrm{4}},{a}+\mathrm{1}\right)−\zeta\left(\frac{\mathrm{3}}{\mathrm{4}},{a}+\mathrm{1}\right)\right) \\ $$$${know}\:{using}\:{Steiljis}\:{constante} \\ $$$$ \\ $$
