Question Number 124360 by Lordose last updated on 02/Dec/20
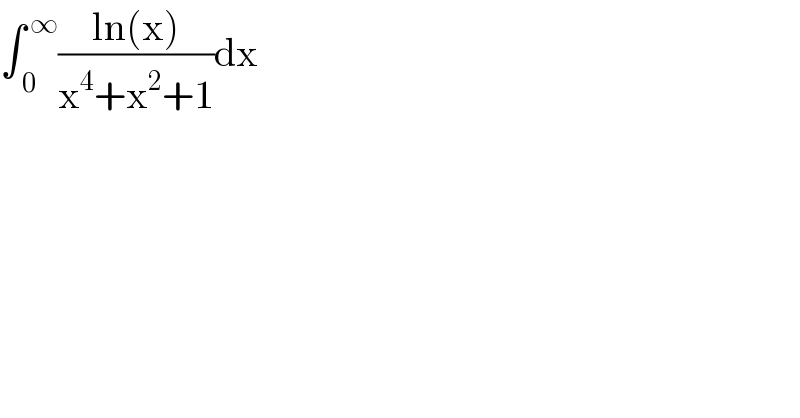
$$\int_{\:\mathrm{0}} ^{\:\infty} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 02/Dec/20

$$\mathrm{we}\:\mathrm{use}\:\int_{\mathrm{0}} ^{\infty} \mathrm{q}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:,\mathrm{a}_{\mathrm{i}} \right)\right. \\ $$$$\mathrm{q}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}\right)=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}=\mathrm{w}\left(\mathrm{z}\right) \\ $$$$\mathrm{z}^{\mathrm{4}} \:+\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}+\mathrm{1}\:\:\left(\mathrm{u}=\mathrm{z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{w}\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}^{\mathrm{2}} \:−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)} \\ $$$$\Sigma\:\mathrm{Res}\left(\mathrm{w}.\right)=\mathrm{Res}\left(\mathrm{w},\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:+\mathrm{Res}\left(\mathrm{w},−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)+\mathrm{Res}\left(\mathrm{w},\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)+\mathrm{Res}\left(\mathrm{w},−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{Res}\left(\mathrm{w},\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)=\frac{\left(\frac{\mathrm{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{36}}\:\frac{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{18i}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\frac{\left(\mathrm{i}\pi+\frac{\mathrm{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}=−\frac{\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{4i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} =\frac{\mathrm{16}\pi^{\mathrm{2}} }{\mathrm{18i}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} =\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\mathrm{w},\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\frac{\left(−\frac{\mathrm{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{36i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{18i}\sqrt{\mathrm{3}}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\frac{\left(\mathrm{i}\pi−\frac{\mathrm{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(−\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}=−\frac{\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{4i}\:.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{18i}\sqrt{\mathrm{3}}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:=−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}\left(\mathrm{w},\mathrm{z}_{\mathrm{i}} \right)\:=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} −\mathrm{i}\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} −\mathrm{i}\frac{\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:+\mathrm{i}\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$=−\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \left(−\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\:+\frac{\mathrm{4i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\mathrm{i}\pi^{\mathrm{2}} }{\:\mathrm{6}\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\:+\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{12}\sqrt{\mathrm{3}}}\:−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow\:\mathrm{I}\:=−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{18}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{24}}−\frac{\pi^{\mathrm{2}} }{\mathrm{36}} \\ $$
