Question Number 151504 by talminator2856791 last updated on 21/Aug/21
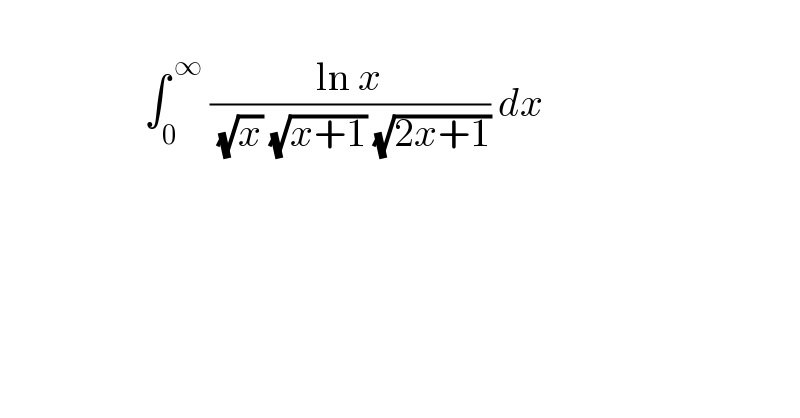
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{ln}\:{x}}{\:\sqrt{{x}}\:\sqrt{{x}+\mathrm{1}}\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:{dx} \\ $$$$\: \\ $$
Answered by Kamel last updated on 21/Aug/21

$$ \\ $$$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{{Ln}\left({x}\right){dx}}{\:\sqrt{{x}}\sqrt{\mathrm{1}+{x}}\sqrt{\mathrm{1}+\mathrm{2}{x}}} \\ $$$$\Omega\overset{{x}=\frac{{t}}{\mathrm{2}}} {=}\int_{\mathrm{0}} ^{+\infty} \frac{{Ln}\left({t}\right)−{Ln}\left(\mathrm{2}\right)}{\:\sqrt{{t}}\sqrt{\mathrm{2}+{t}}\sqrt{\mathrm{1}+{t}}}{dt}=−\int_{\mathrm{0}} ^{+\infty} \frac{{Ln}\left({t}\right){dt}}{\:\sqrt{{t}}\sqrt{\mathrm{1}+\mathrm{2}{t}}\sqrt{\mathrm{1}+{t}}}−\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{Ln}\left(\mathrm{2}\right){du}}{\:\sqrt{{u}^{\mathrm{2}} +\mathrm{2}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$\therefore\:\Omega={Ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{+\infty} \frac{{du}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\sqrt{\mathrm{1}+\mathrm{2}{u}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\overset{{u}={tg}\left({t}\right)} {=}{Ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\:\sqrt{{cos}^{\mathrm{2}} \left({t}\right)+\mathrm{2}{sin}^{\mathrm{2}} \left({t}\right)}} \\ $$$$\:\:\:\:\:\:\:\:\:={Ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\:\sqrt{\mathrm{2}−{cos}^{\mathrm{2}} \left({t}\right)}}\overset{\theta=\frac{\pi}{\mathrm{2}}−{t}} {=}\frac{{Ln}\left(\mathrm{2}\right)}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\theta\right)}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{{K}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}{Ln}\left(\mathrm{2}\right) \\ $$
