Question Number 122980 by liberty last updated on 21/Nov/20
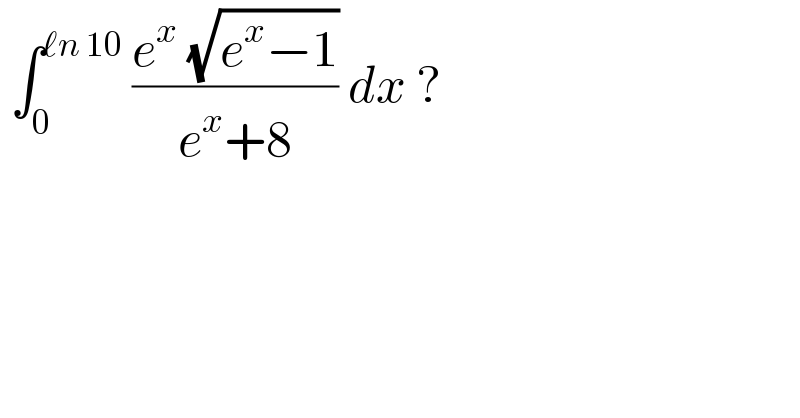
$$\:\int_{\mathrm{0}} ^{\ell{n}\:\mathrm{10}} \:\frac{{e}^{{x}} \:\sqrt{{e}^{{x}} −\mathrm{1}}}{{e}^{{x}} +\mathrm{8}}\:{dx}\:? \\ $$
Answered by bemath last updated on 21/Nov/20
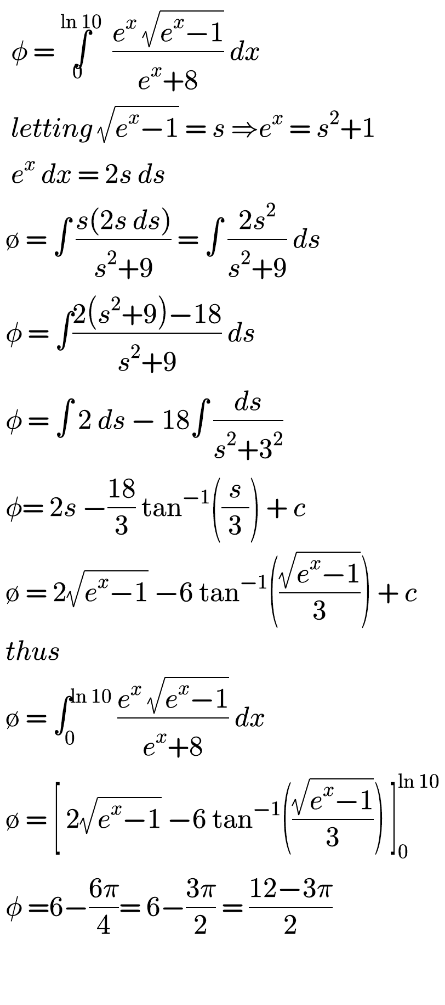
Answered by mathmax by abdo last updated on 21/Nov/20
![I =∫_0 ^(ln(10)) ((e^x (√(e^x −1)))/(e^x +8))dx changement (√(e^x −1))=t give e^x −1 =t^2 ⇒e^x =t^2 +1 ⇒x=ln(t^2 +1) ⇒ I =∫_0 ^3 (((t^2 +1)t)/(t^2 +1+8))×((2tdt)/(t^2 +1)) =∫_0 ^3 ((2t^2 )/(t^2 +9))dt =2∫_0 ^3 ((t^2 +9−9)/(t^2 +9))dt =2∫_0 ^3 dt −18∫_0 ^3 (dt/(t^2 +9))(→t=3u) =6−18 ∫_0 ^1 ((3du)/(9(1+u^2 ))) =6−6 ∫_0 ^1 (du/(1+u^2 )) =6−6[arctanu]_0 ^1 =6−6.(π/4) =6−((3π)/2)](https://www.tinkutara.com/question/Q122991.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{10}\right)} \:\frac{\mathrm{e}^{\mathrm{x}} \sqrt{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}}{\mathrm{e}^{\mathrm{x}} \:+\mathrm{8}}\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{e}^{\mathrm{x}} −\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow\mathrm{x}=\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{8}}×\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{9}−\mathrm{9}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{dt}\:−\mathrm{18}\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{9}}\left(\rightarrow\mathrm{t}=\mathrm{3u}\right) \\ $$$$=\mathrm{6}−\mathrm{18}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{3du}}{\mathrm{9}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:=\mathrm{6}−\mathrm{6}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\mathrm{6}−\mathrm{6}\left[\mathrm{arctanu}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{6}−\mathrm{6}.\frac{\pi}{\mathrm{4}}\:=\mathrm{6}−\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$
