Question Number 117002 by TANMAY PANACEA last updated on 08/Oct/20
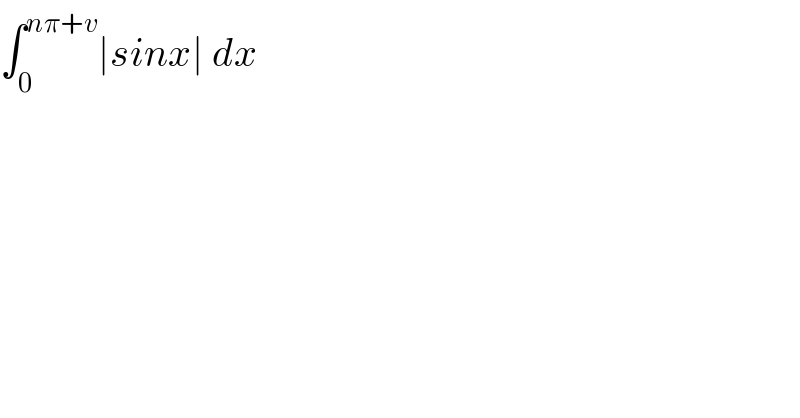
$$\int_{\mathrm{0}} ^{{n}\pi+{v}} \mid{sinx}\mid\:{dx} \\ $$
Answered by TANMAY PANACEA last updated on 08/Oct/20

$$\mid{sinx}\mid\:{is}\:{alsays}\:+{ve}\:{and}\:{each}\:{loop}\:{area}\:{of} \\ $$$${sinx}\:{is}\:\mathrm{2}\:\:\bigstar\bigstar\: \\ $$$$\int_{\mathrm{0}} ^{\pi} {sinx}\:{dx}=−\mid{cosx}\mid_{\mathrm{0}} ^{\pi} =\mathrm{2} \\ $$$$\bigstar\bigstar \\ $$$${now}\:{look} \\ $$$$\int_{\mathrm{0}} ^{{n}\pi+{v}} \mid{sinx}\mid{dx}=\int_{\mathrm{0}} ^{{v}} \mid{sinx}\mid{dx}+\int_{{v}} ^{{n}\pi+{v}} \mid{sinx}\mid{dx} \\ $$$${here}\:\mathrm{0}<{v}<\pi \\ $$$$\int_{\mathrm{0}} ^{{v}} {sinx}\:{dx}=−\mid{cosx}\mid_{\mathrm{0}} ^{{v}} =−\left({cozv}−\mathrm{1}\right)=\mathrm{1}−{cosv} \\ $$$$\int_{{v}} ^{{n}\pi+{v}} \mid{sinx}\mid{dx}\rightarrow{in}\:{interval}\:{v}\:{to}\:{v}+{n}\pi \\ $$$${n}\:{umber}\:{of}\:{loop}\:{so} \\ $$$$\int_{{v}} ^{{n}\pi+{v}} \:\mid{sinx}\mid{dx}={n}×\mathrm{2}=\mathrm{2}{n} \\ $$$$\boldsymbol{{I}}=\mathrm{2}{n}+\mathrm{1}−{cosv} \\ $$$${plz}\:{check} \\ $$
