Question Number 184626 by SANOGO last updated on 09/Jan/23
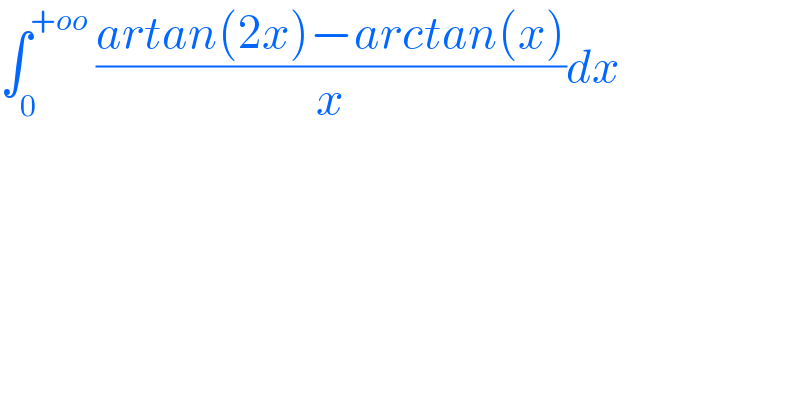
$$\int_{\mathrm{0}} ^{+{oo}} \:\frac{{artan}\left(\mathrm{2}{x}\right)−{arctan}\left({x}\right)}{{x}}{dx} \\ $$
Answered by qaz last updated on 10/Jan/23
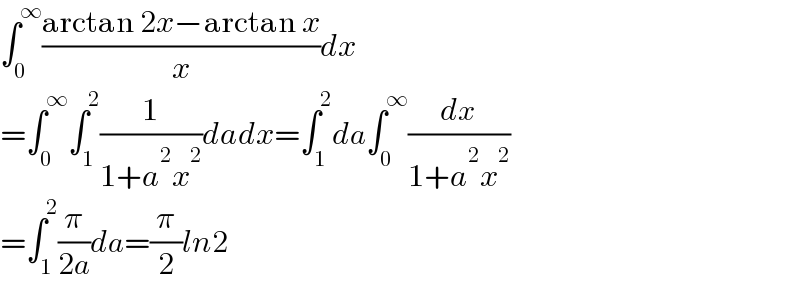
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{arctan}\:\mathrm{2}{x}−\mathrm{arctan}\:{x}}{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }{dadx}=\int_{\mathrm{1}} ^{\mathrm{2}} {da}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\pi}{\mathrm{2}{a}}{da}=\frac{\pi}{\mathrm{2}}{ln}\mathrm{2} \\ $$
