0-pi-1-1-cos-2-x-dx-

Question Number 146371 by lapache last updated on 13/Jul/21

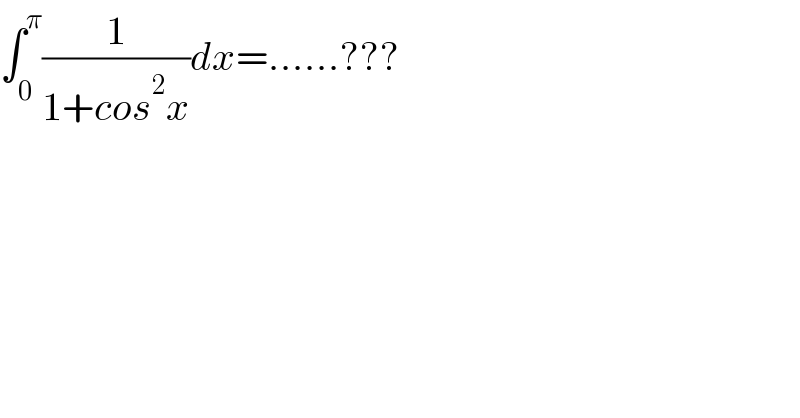
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx}=……??? \\ $$

Answered by gsk2684 last updated on 13/Jul/21

let I=∫_0 ^Π (1/(1+cos^2 x)) dx (1) f(Π−x)=(1/(1+cos^2 (Π−x))) =(1/(1+cos^2 x))=f(x) (1)⇒I=2∫_0 ^(Π/2) (1/(1+cos^2 x))dx ⇒I=2∫_0 ^(Π/2) (1/(sec^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(1+tan^2 x+1)) sec^2 x dx ⇒I=2∫_0 ^(Π/2) (1/(tan^2 x+((√2))^2 )) d(tan x) ⇒I=2[(1/( (√2)))tan^(−1) (((tan x)/( (√2))))]_0 ^(Π/2) ⇒I=(√2)[(Π/2)−0]=(Π/( (√2)))

$${let}\:{I}=\underset{\mathrm{0}} {\overset{\Pi} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:\:\:\left(\mathrm{1}\right) \\ $$$${f}\left(\Pi−{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \left(\Pi−{x}\right)}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}={f}\left({x}\right) \\ $$$$\left(\mathrm{1}\right)\Rightarrow{I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\Pi}{\mathrm{2}}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}{dx} \\ $$$$\Rightarrow{I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\Pi}{\mathrm{2}}} {\int}}\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} {x}+\mathrm{1}}\:\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx} \\ $$$$\Rightarrow{I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\Pi}{\mathrm{2}}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{1}}\:\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx} \\ $$$$\Rightarrow{I}=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\Pi}{\mathrm{2}}} {\int}}\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:{d}\left({tan}\:{x}\right) \\ $$$$\Rightarrow{I}=\mathrm{2}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$\Rightarrow{I}=\sqrt{\mathrm{2}}\left[\frac{\Pi}{\mathrm{2}}−\mathrm{0}\right]=\frac{\Pi}{\:\sqrt{\mathrm{2}}} \\ $$

Answered by Ar Brandon last updated on 13/Jul/21

I=∫_0 ^π (dx/(1+cos^2 x))=2∫_0 ^(π/2) ((sec^2 x)/(sec^2 x+1))dx =2∫_0 ^(π/2) ((d(tanx))/(2+tan^2 x))=(2/( (√2)))[arctan(((tanx)/( (√2))))]_0 ^(π/2) =(π/( (√2)))

$$\mathrm{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\mathrm{2}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{arctan}\left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$

Answered by mathmax by abdo last updated on 13/Jul/21

Ψ=∫_0 ^π (dx/(1+cos^2 x)) ⇒Ψ=∫_0 ^π (dx/(1+((1+cos(2x))/2)))=∫_0 ^π ((2dx)/(3+cos(2x))) =_(2x=t) ∫_0 ^(2π) (dt/(3+cost))=_(e^(it) =z) ∫_(∣z∣=1) (dz/(iz(3+((z+z^(−1) )/2)))) =∫ ((−2idz)/(z(6+z+z^(−1) )))=∫_(∣z∣=1) ((−2idz)/(z^2 +6z +1))=∫_(∣z∣=1) ϕ(z)dz Δ^′ =9−1=8 ⇒z_1 =−3+2(√2) and z_2 =−3−2(√2) ∣z_1 ∣−1=3−2(√2)−1 =2−2(√2)<0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1=3+2(√2)−1=2+2(√2)>0 ⇒∣z_2 ∣>1 residus theoem ⇒ ∫_(∣z∣=1) ϕ(z)dz=2iπ Res(ϕ,z_1 ) ϕ(z)=((−2i)/((z−z_1 )(z−z_2 ))) ⇒Res(ϕ,z_1 )=((−2i)/(z_1 −z_2 ))=((−2i)/(4(√2)))=((−i)/(2(√2))) ⇒ ∫_(∣z∣=1) ϕ(z)dz=2iπ×((−i)/(2(√2))) =(π/( (√2))) ⇒Ψ=(π/( (√2)))

$$\Psi=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\Psi=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{1}+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{2dx}}{\mathrm{3}+\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$$$=_{\mathrm{2x}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{3}+\mathrm{cost}}=_{\mathrm{e}^{\mathrm{it}} \:=\mathrm{z}} \:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{3}+\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=\int\:\:\frac{−\mathrm{2idz}}{\mathrm{z}\left(\mathrm{6}+\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)}=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{−\mathrm{2idz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{6z}\:+\mathrm{1}}=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz} \\ $$$$\Delta^{'} \:=\mathrm{9}−\mathrm{1}=\mathrm{8}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}<\mathrm{0}\:\Rightarrow\mid\mathrm{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}=\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}>\mathrm{0}\:\Rightarrow\mid\mathrm{z}_{\mathrm{2}} \mid>\mathrm{1}\:\mathrm{residus}\:\mathrm{theoem}\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right) \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{−\mathrm{2i}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\Rightarrow\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)=\frac{−\mathrm{2i}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }=\frac{−\mathrm{2i}}{\mathrm{4}\sqrt{\mathrm{2}}}=\frac{−\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{2i}\pi×\frac{−\mathrm{i}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\Psi=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$

Facebook Tweet Pin

0-pi-1-1-cos-2-x-dx-

Leave a Reply Cancel reply