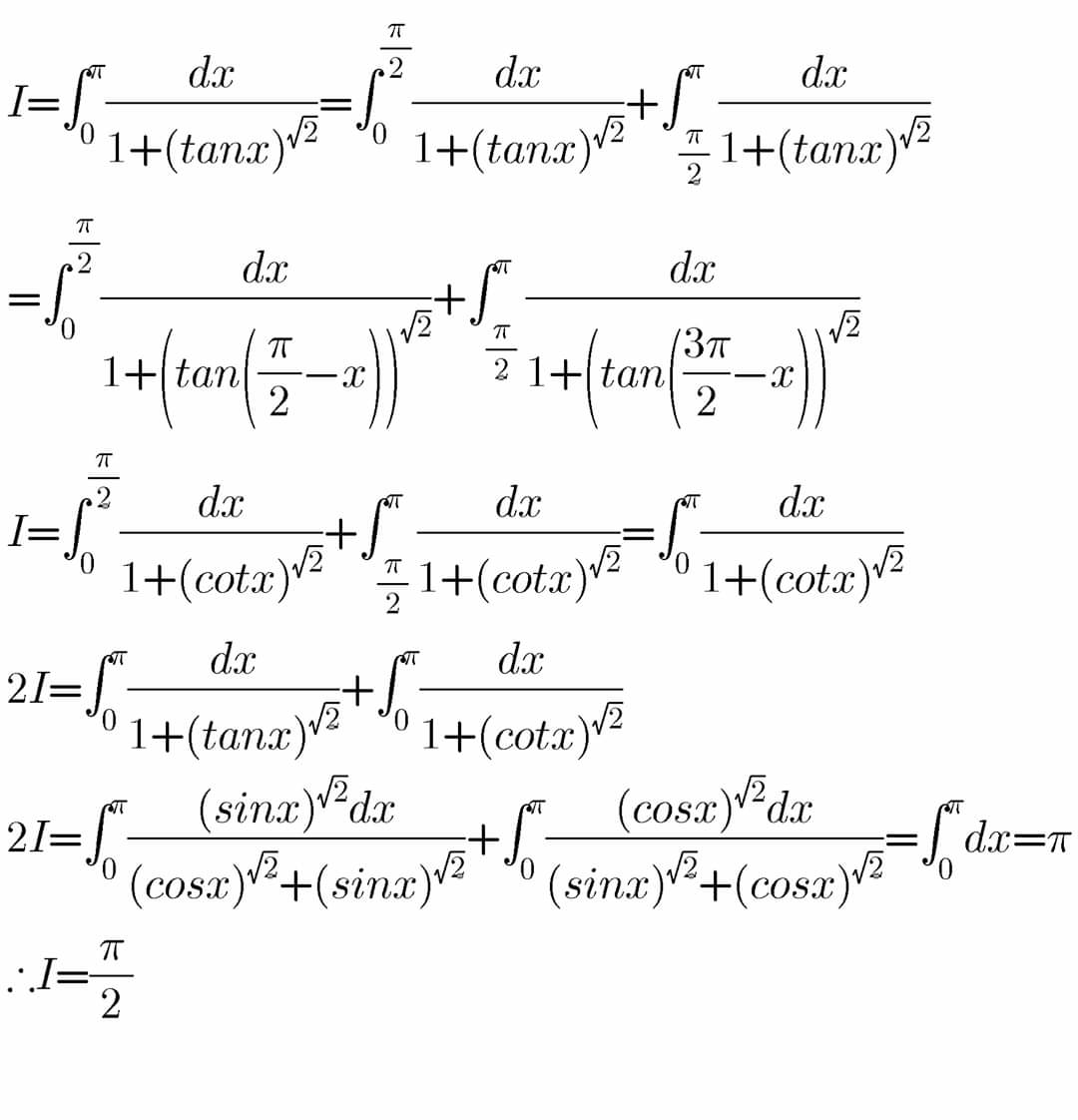Question Number 82450 by M±th+et£s last updated on 21/Feb/20
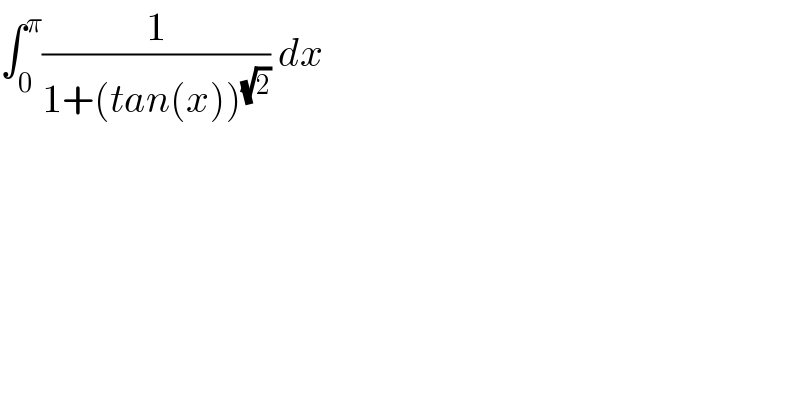
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\mathrm{1}+\left({tan}\left({x}\right)\right)^{\sqrt{\mathrm{2}}} }\:{dx} \\ $$
Commented by MJS last updated on 21/Feb/20
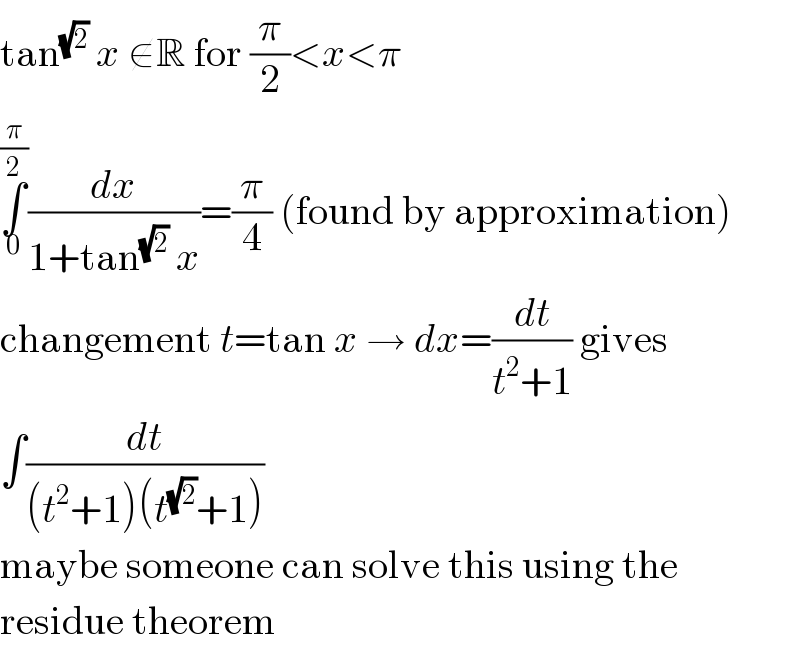
$$\mathrm{tan}^{\sqrt{\mathrm{2}}} \:{x}\:\notin\mathbb{R}\:\mathrm{for}\:\frac{\pi}{\mathrm{2}}<{x}<\pi \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{dx}}{\mathrm{1}+\mathrm{tan}^{\sqrt{\mathrm{2}}} \:{x}}=\frac{\pi}{\mathrm{4}}\:\left(\mathrm{found}\:\mathrm{by}\:\mathrm{approximation}\right) \\ $$$$\mathrm{changement}\:{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{gives} \\ $$$$\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\sqrt{\mathrm{2}}} +\mathrm{1}\right)} \\ $$$$\mathrm{maybe}\:\mathrm{someone}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{using}\:\mathrm{the} \\ $$$$\mathrm{residue}\:\mathrm{theorem} \\ $$
Answered by M±th+et£s last updated on 22/Feb/20