Question Number 166612 by mnjuly1970 last updated on 23/Feb/22
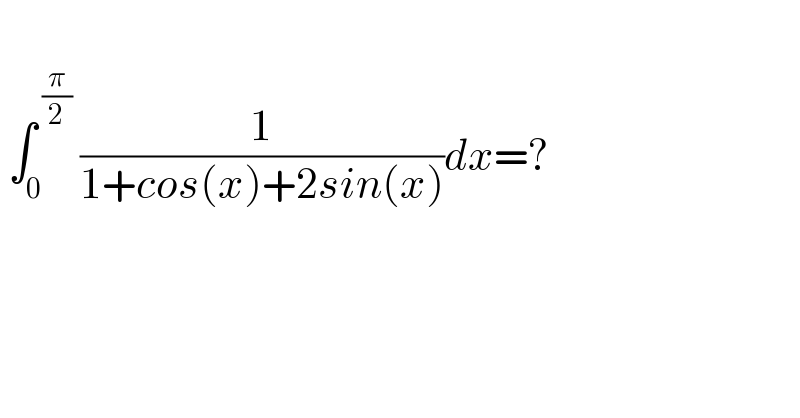
$$ \\ $$$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{1}+{cos}\left({x}\right)+\mathrm{2}{sin}\left({x}\right)}{dx}=? \\ $$
Commented by cortano1 last updated on 23/Feb/22
![1+cos x+2sin x= cos^2 (1/2)x+sin^2 (1/2)x+cos^2 (1/2)x−sin^2 (1/x)+2sin x = 2cos^2 (1/2)x+4sin (1/2)xcos (1/2)x = 2cos (1/2)x(cos (1/2)x+2sin (1/2)x) I=(1/2)∫ ((sec (1/2)x)/(cos (1/2)x+2sin (1/2)x)) dx I=(1/2)∫ ((sec^2 (1/2)x)/(1+2tan (1/2)x)) dx [ u=(1/2)x ] I= ∫ ((sec^2 u)/(1+2tan u)) du = (1/2)∫ ((d(1+2tan u))/(1+2tan u)) I=(1/2) ln ∣ 1+2tan u ∣ +c I= (1/2)ln ∣1+2tan (1/2)x∣ + c ∫_0 ^( (π/2)) (dx/(1+cos x+2sin x)) =(1/2) [ ln ∣1+2tan (1/2)x∣]_0 ^(π/2) = ((ln 3)/2) .](https://www.tinkutara.com/question/Q166613.png)
$$\:\mathrm{1}+\mathrm{cos}\:\mathrm{x}+\mathrm{2sin}\:\mathrm{x}=\:\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}}+\mathrm{2sin}\:\mathrm{x} \\ $$$$=\:\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{4sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{xcos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x} \\ $$$$=\:\mathrm{2cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\left(\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right) \\ $$$$\:\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{sec}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}\:\mathrm{dx} \\ $$$$\:\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{1}+\mathrm{2tan}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\:\left[\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\right] \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}}{\mathrm{1}+\mathrm{2tan}\:\mathrm{u}}\:\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{2tan}\:\mathrm{u}\right)}{\mathrm{1}+\mathrm{2tan}\:\mathrm{u}} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid\:\mathrm{1}+\mathrm{2tan}\:\mathrm{u}\:\mid\:+\mathrm{c} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+\mathrm{2tan}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\mid\:+\:\mathrm{c} \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}+\mathrm{2sin}\:\mathrm{x}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{ln}\:\mid\mathrm{1}+\mathrm{2tan}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:=\:\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{2}}\:. \\ $$
Commented by peter frank last updated on 23/Feb/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by MJS_new last updated on 23/Feb/22
![∫_0 ^(π/2) (dx/(1+cos x +2sin x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =∫_0 ^1 (dt/(2t+1))=(1/2)[ln (2t+1)]_0 ^1 =((ln 3)/2)](https://www.tinkutara.com/question/Q166634.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{1}+\mathrm{cos}\:{x}\:+\mathrm{2sin}\:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\left(\mathrm{2}{t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{2}} \\ $$
