Question Number 53295 by gunawan last updated on 20/Jan/19
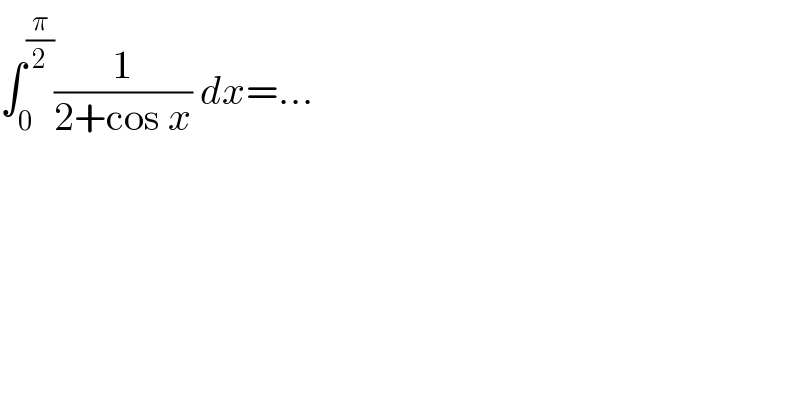
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+\mathrm{cos}\:{x}}\:{dx}=… \\ $$
Commented by maxmathsup by imad last updated on 20/Jan/19
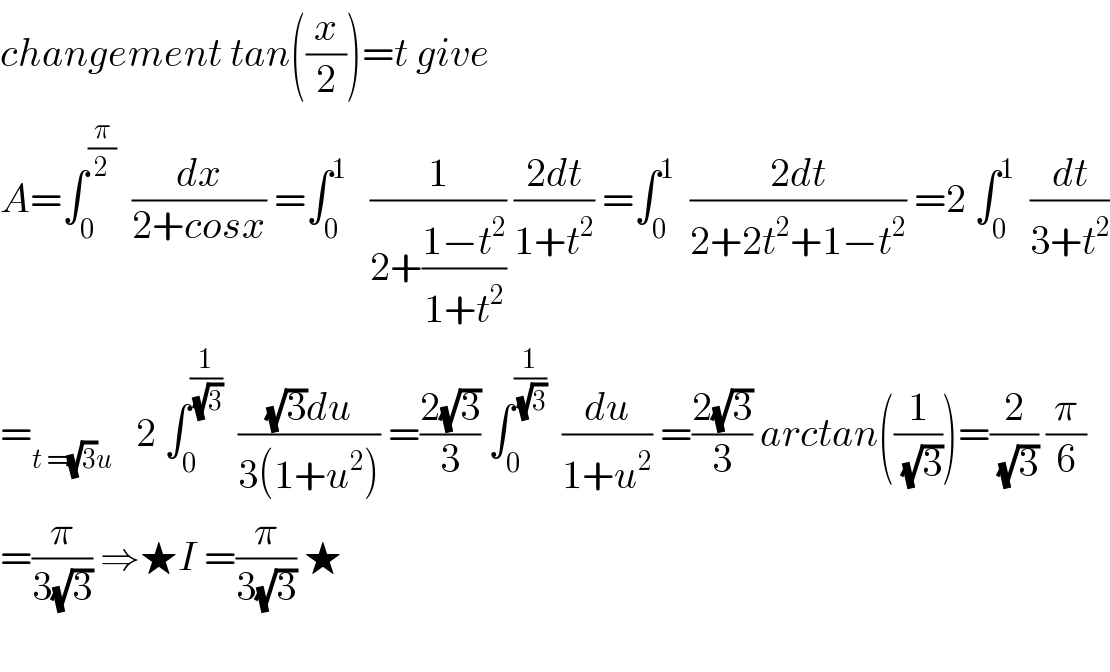
$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\: \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{2}+{cosx}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}−{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{3}+{t}^{\mathrm{2}} } \\ $$$$=_{{t}\:=\sqrt{\mathrm{3}}{u}} \:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\frac{\sqrt{\mathrm{3}}{du}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\frac{\pi}{\mathrm{6}} \\ $$$$=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow\bigstar{I}\:=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\bigstar \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19
![∫_0 ^(π/2) (1/(2+((1−tan^2 (x/2))/(1+tan^2 (x/2)))))dx ∫_0 ^(π/2) ((sec^2 (x/2))/(2+2tan^2 (x/(2 ))+1−tan^2 (x/2)))dx t=tan(x/2) dt=(1/2)sec^2 (x/2)dx ∫_0 ^1 ((2dt)/(3+t^2 )) 2×(1/( (√3)))∣tan^(−1) ((t/( (√3))))∣_0 ^1 (2/( (√3)))[tan^(−1) ((1/( (√3))))]=(2/( (√3)))×(π/6)=(π/(3(√3)))](https://www.tinkutara.com/question/Q53297.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}+\mathrm{2}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}\:}+\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:\:\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dt}}{\mathrm{3}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\mathrm{3}}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{6}}=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by gunawan last updated on 20/Jan/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
