Question Number 83781 by john santu last updated on 06/Mar/20
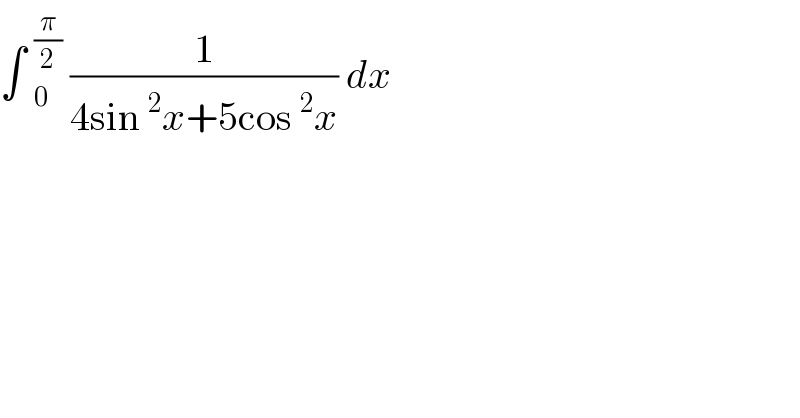
$$\int\:_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{4sin}\:^{\mathrm{2}} {x}+\mathrm{5cos}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$
Commented by niroj last updated on 06/Mar/20
![∫_0 ^(π/2) (( 1)/(4sin^2 x+5cos^2 x))dx = ∫_0 ^(π/2) (( sec^2 x dx)/( 4tan^2 x+5)) put tan x=t sec^2 xdx=dt if x=(π/2)then t=∞ if x=0 then t=0 = ∫_0 ^( ∞) (1/(4t^2 +5))dt = (1/4)∫_0 ^( ∞) (1/(t^2 +(5/4)))dt = (1/4)[∫ (1/((t)^2 +(((√5)/2))^2 ))dt]_0 ^∞ = (1/4)[ (1/((√5)/2)) tan^(−1) (t/((√5)/2))]_0 ^∞ = (1/4)[ (2/( (√5)))tan^(−1) (∞).(2/( (√5)))−0] = (1/4).(2/( (√5))). (π/2)= (π/(4(√5)))//.](https://www.tinkutara.com/question/Q83784.png)
$$\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\:\:\mathrm{1}}{\mathrm{4sin}^{\mathrm{2}} \mathrm{x}+\mathrm{5cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\:\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\:\mathrm{4tan}^{\mathrm{2}} \mathrm{x}+\mathrm{5}} \\ $$$$\:\:\mathrm{put}\:\mathrm{tan}\:\mathrm{x}=\mathrm{t} \\ $$$$\:\:\:\:\:\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{dt} \\ $$$$\:\mathrm{if}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}\mathrm{then}\:\mathrm{t}=\infty \\ $$$$\:\mathrm{if}\:\mathrm{x}=\mathrm{0}\:\mathrm{then}\:\mathrm{t}=\mathrm{0} \\ $$$$\:\:=\:\:\int_{\mathrm{0}} ^{\:\infty} \:\:\frac{\mathrm{1}}{\mathrm{4t}^{\mathrm{2}} +\mathrm{5}}\mathrm{dt} \\ $$$$\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{4}}}\mathrm{dt} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\int\:\frac{\mathrm{1}}{\left(\mathrm{t}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{dt}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{t}}{\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{tan}^{−\mathrm{1}} \left(\infty\right).\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}−\mathrm{0}\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}.\:\frac{\pi}{\mathrm{2}}=\:\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{5}}}//. \\ $$$$ \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\: \\ $$$$ \\ $$
Commented by john santu last updated on 06/Mar/20
![in short cut = ∫ _0^(π/2) (dx/(a^2 sin^2 x+b^2 cos^2 x)) = (π/(2ab)) [ a=(√4) = 2 , b =(√5) ] = (π/(2.2.(√5))) = (π/(4(√5))) ★](https://www.tinkutara.com/question/Q83785.png)
$$\mathrm{in}\:\mathrm{short}\:\mathrm{cut}\: \\ $$$$=\:\int\:_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$=\:\frac{\pi}{\mathrm{2ab}}\:\left[\:\mathrm{a}=\sqrt{\mathrm{4}}\:=\:\mathrm{2}\:,\:\mathrm{b}\:=\sqrt{\mathrm{5}}\:\right] \\ $$$$=\:\frac{\pi}{\mathrm{2}.\mathrm{2}.\sqrt{\mathrm{5}}}\:=\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{5}}}\:\bigstar\: \\ $$
Answered by MJS last updated on 06/Mar/20
![∫(dx/(4sin^2 x +5cos^2 x))= [t=tan x → dx=(dt/(t^2 +1)); sin x =(t/( (√(t^2 +1)))); cos x =(1/( (√(t^2 +1))))] =∫(dt/(4t^2 +5))=((√5)/(10))arctan ((2(√5)t)/5) = =((√5)/(10))arctan ((2(√5)tan x)/5) +C snswer is ((π(√5))/(20))](https://www.tinkutara.com/question/Q83801.png)
$$\int\frac{{dx}}{\mathrm{4sin}^{\mathrm{2}} \:{x}\:+\mathrm{5cos}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}};\:\mathrm{sin}\:{x}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}};\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{5}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\mathrm{arctan}\:\frac{\mathrm{2}\sqrt{\mathrm{5}}{t}}{\mathrm{5}}\:= \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\mathrm{arctan}\:\frac{\mathrm{2}\sqrt{\mathrm{5}}\mathrm{tan}\:{x}}{\mathrm{5}}\:+{C} \\ $$$$\mathrm{snswer}\:\mathrm{is}\:\frac{\pi\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$
