Menu Close

0-pi-2-1-sin-x-sin-2-x-sin-3-x-sin-4-x-sin-5-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 128664 by bemath last updated on 09/Jan/21
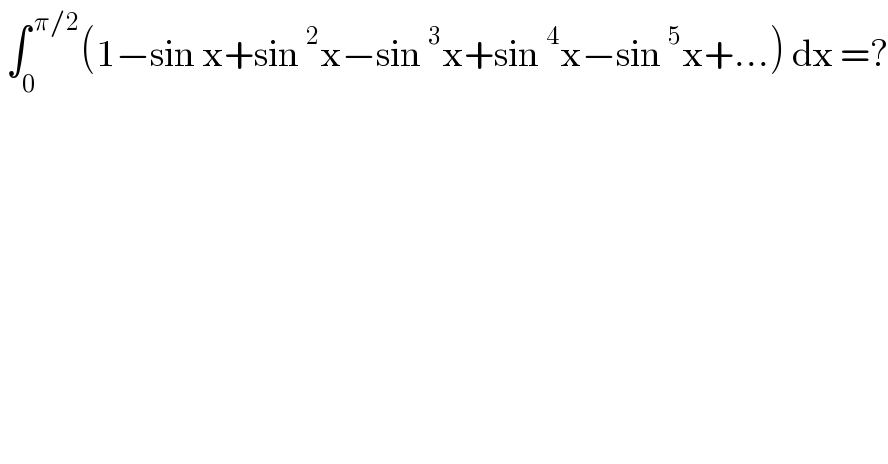
∫_0 ^( π/2) (1−sin x+sin^2 x−sin^3 x+sin^4 x−sin^5 x+...) dx =?
$$\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{5}} \mathrm{x}+…\right)\:\mathrm{dx}\:=? \\ $$
Answered by liberty last updated on 09/Jan/21
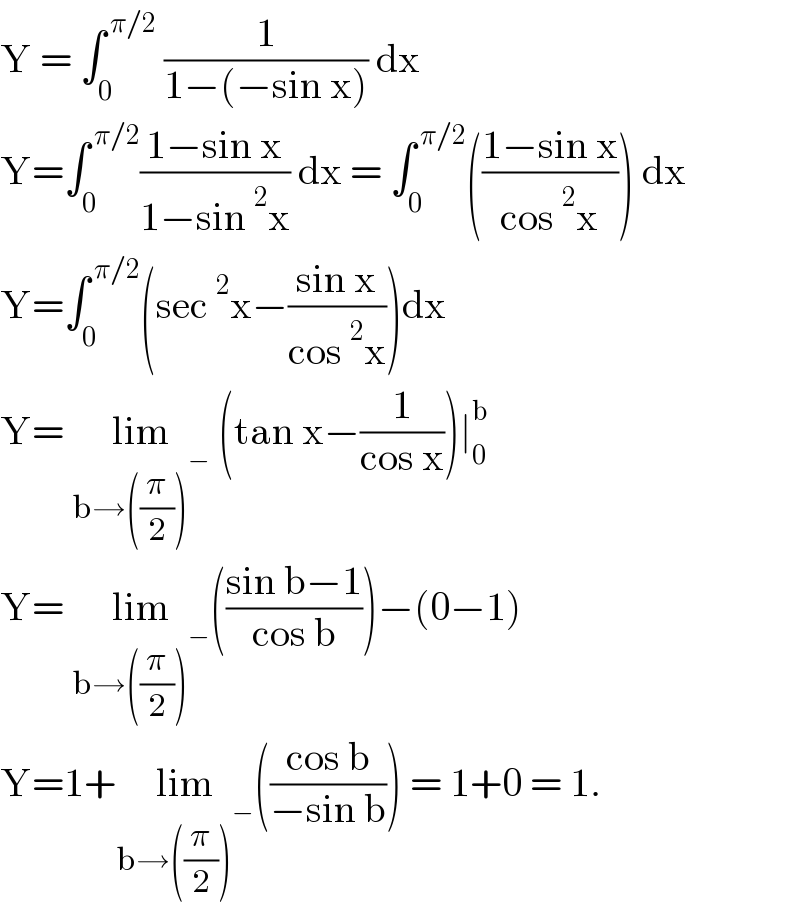
Y = ∫_0 ^( π/2) (1/(1−(−sin x))) dx Y=∫_0 ^( π/2) ((1−sin x)/(1−sin^2 x)) dx = ∫_0 ^( π/2) (((1−sin x)/(cos^2 x))) dx Y=∫_0 ^( π/2) (sec^2 x−((sin x)/(cos^2 x)))dx Y= lim_(b→((π/2))^− ) (tan x−(1/(cos x)))∣_0 ^b Y= lim_(b→((π/2))^− ) (((sin b−1)/(cos b)))−(0−1) Y=1+lim_(b→((π/2))^− ) (((cos b)/(−sin b))) = 1+0 = 1.
$$\mathrm{Y}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{1}−\left(−\mathrm{sin}\:\mathrm{x}\right)}\:\mathrm{dx}\: \\ $$$$\mathrm{Y}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\right)\:\mathrm{dx}\: \\ $$$$\mathrm{Y}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx}\: \\ $$$$\mathrm{Y}=\:\underset{\mathrm{b}\rightarrow\left(\frac{\pi}{\mathrm{2}}\right)^{−} } {\mathrm{lim}}\:\left(\mathrm{tan}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}\right)\mid_{\mathrm{0}} ^{\mathrm{b}} \\ $$$$\mathrm{Y}=\:\underset{\mathrm{b}\rightarrow\left(\frac{\pi}{\mathrm{2}}\right)^{−} } {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\mathrm{b}−\mathrm{1}}{\mathrm{cos}\:\mathrm{b}}\right)−\left(\mathrm{0}−\mathrm{1}\right) \\ $$$$\mathrm{Y}=\mathrm{1}+\underset{\mathrm{b}\rightarrow\left(\frac{\pi}{\mathrm{2}}\right)^{−} } {\mathrm{lim}}\left(\frac{\mathrm{cos}\:\mathrm{b}}{−\mathrm{sin}\:\mathrm{b}}\right)\:=\:\mathrm{1}+\mathrm{0}\:=\:\mathrm{1}. \\ $$
Answered by Dwaipayan Shikari last updated on 09/Jan/21
∫_0 ^(π/2) (1/(1+sinx))dx =2∫_0 ^1 (1/(1+((2t)/(1+t^2 )))).(1/(1+t^2 ))dt t=tan(x/2) =−[(2/((1+t)))]_0 ^1 =1
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+{sinx}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\:{t}={tan}\frac{{x}}{\mathrm{2}} \\ $$$$=−\left[\frac{\mathrm{2}}{\left(\mathrm{1}+{t}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *