Question Number 163496 by Ahmed777hamouda last updated on 07/Jan/22
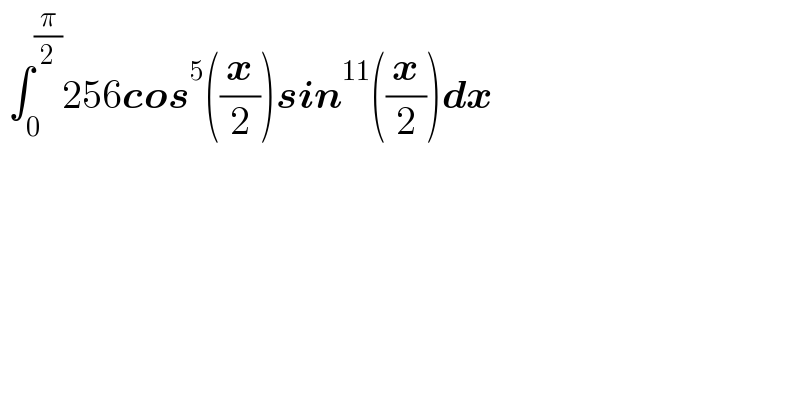
$$\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{256}\boldsymbol{{cos}}^{\mathrm{5}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\boldsymbol{{sin}}^{\mathrm{11}} \left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\boldsymbol{{dx}} \\ $$
Answered by Ar Brandon last updated on 07/Jan/22
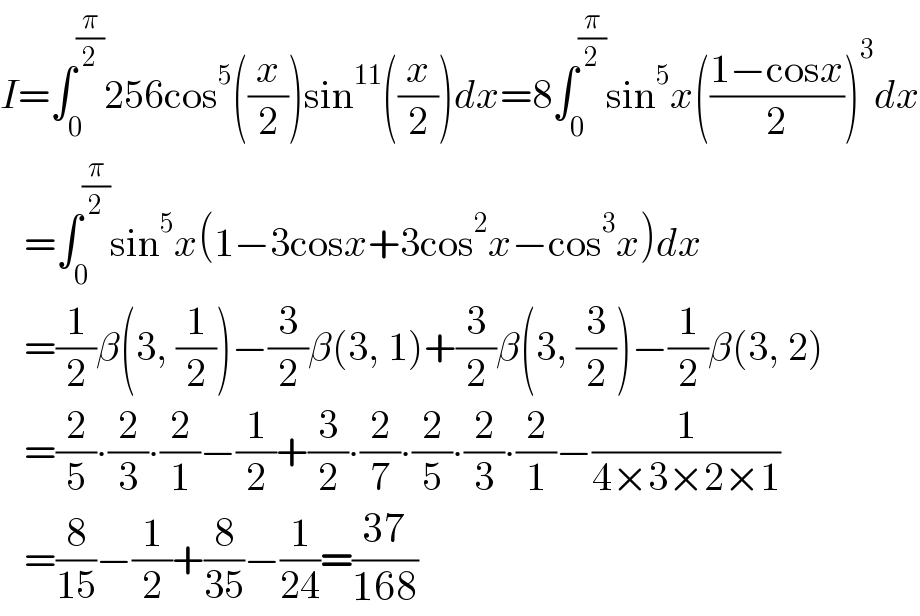
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{256cos}^{\mathrm{5}} \left(\frac{{x}}{\mathrm{2}}\right)\mathrm{sin}^{\mathrm{11}} \left(\frac{{x}}{\mathrm{2}}\right){dx}=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{5}} {x}\left(\frac{\mathrm{1}−\mathrm{cos}{x}}{\mathrm{2}}\right)^{\mathrm{3}} {dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{5}} {x}\left(\mathrm{1}−\mathrm{3cos}{x}+\mathrm{3cos}^{\mathrm{2}} {x}−\mathrm{cos}^{\mathrm{3}} {x}\right){dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\mathrm{3},\:\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{3}}{\mathrm{2}}\beta\left(\mathrm{3},\:\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}}\beta\left(\mathrm{3},\:\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\mathrm{3},\:\mathrm{2}\right) \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{2}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{7}}\centerdot\frac{\mathrm{2}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{2}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}} \\ $$$$\:\:\:=\frac{\mathrm{8}}{\mathrm{15}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{8}}{\mathrm{35}}−\frac{\mathrm{1}}{\mathrm{24}}=\frac{\mathrm{37}}{\mathrm{168}} \\ $$
