Question Number 187458 by mnjuly1970 last updated on 17/Feb/23
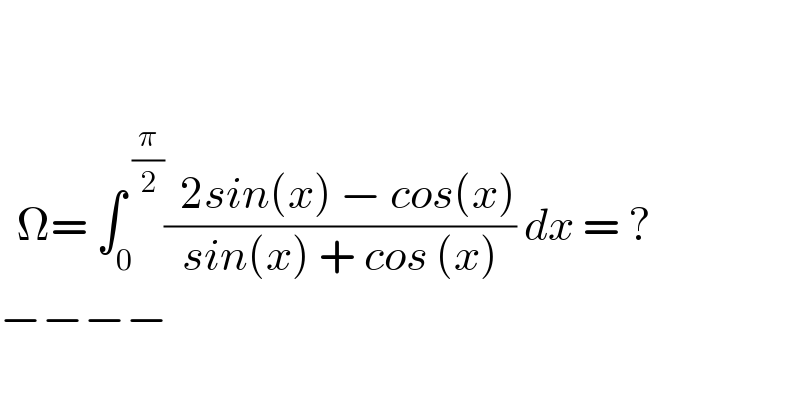
$$ \\ $$$$ \\ $$$$\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\:\:\mathrm{2}{sin}\left({x}\right)\:−\:{cos}\left({x}\right)}{{sin}\left({x}\right)\:+\:{cos}\:\left({x}\right)}\:{dx}\:=\:? \\ $$$$−−−− \\ $$
Answered by Frix last updated on 17/Feb/23
![((2sin x −cos x)/(sin x +cos x))−(1/2)+(1/2)= =((3(sin x −cos x))/(2(sin x +cos x)))+(1/2)= =(1/2)−((3(√2)cos (x+(π/4)))/(2(√2)sin (x+(π/4)))) ∫_0 ^(π/2) ((1/2)−(3/2)cot (x+(π/4)))dx= =[(x/2)−((3ln ∣sin (x+(π/4))∣)/2)]_0 ^(π/2) =(π/4)](https://www.tinkutara.com/question/Q187461.png)
$$\frac{\mathrm{2sin}\:{x}\:−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{3}\left(\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right)}{\mathrm{2}\left(\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\right)}+\frac{\mathrm{1}}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cot}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\right){dx}= \\ $$$$=\left[\frac{{x}}{\mathrm{2}}−\frac{\mathrm{3ln}\:\mid\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\mid}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 17/Feb/23

$${thanks}\:{alot} \\ $$
Answered by anurup last updated on 17/Feb/23
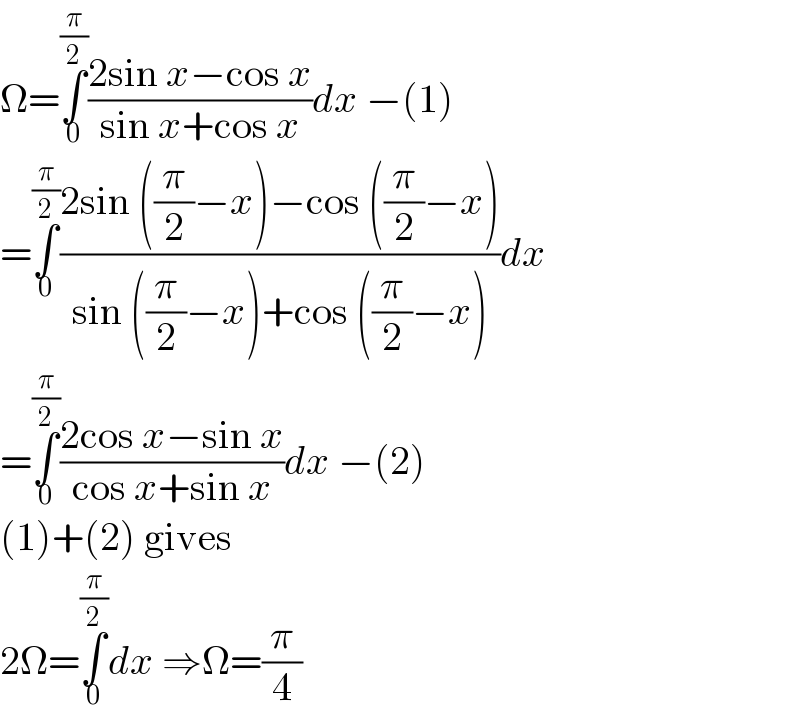
$$\Omega=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{2sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx}\:−\left(\mathrm{1}\right) \\ $$$$=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)+\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{2cos}\:{x}−\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{dx}\:−\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\mathrm{gives} \\ $$$$\mathrm{2}\Omega=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}{dx}\:\Rightarrow\Omega=\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 17/Feb/23
$${thank}\:{you}\:{so}\:{much} \\ $$
