Menu Close

0-pi-2-arc-tan-2-tan-x-tan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 87025 by john santu last updated on 02/Apr/20
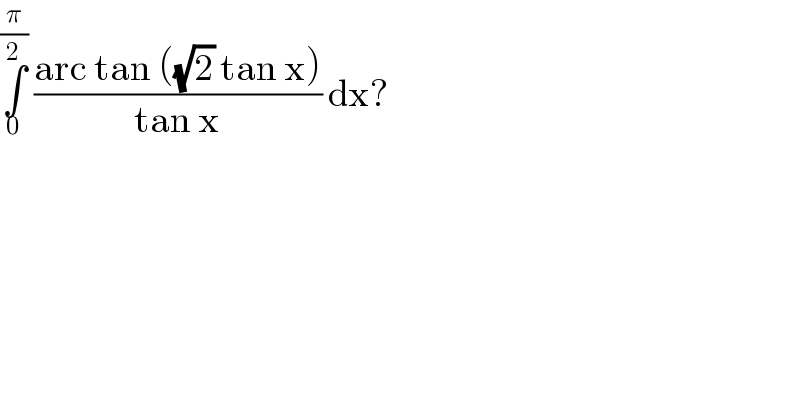
∫_0 ^(π/2) ((arc tan ((√2) tan x))/(tan x)) dx?
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{arc}\:\mathrm{tan}\:\left(\sqrt{\mathrm{2}}\:\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}?\: \\ $$
Commented by mathmax by abdo last updated on 02/Apr/20
let f(a) =∫_0 ^(π/2) ((arctan(atanx))/(tanx))dx with a>0 f^′ (a) =∫_0 ^(π/2) ((tanx)/((1+a^2 tan^2 x)tanx))dx =∫_0 ^(π/2) (dx/(1+a^2 tan^2 x)) =_(atanx =t) ∫_0 ^(+∞) (1/(1+t^2 ))×(1/(a(1+(t^2 /a^2 ))))dt =a∫_0 ^∞ (dt/((t^2 +1)(t^2 +a^2 ))) =(a/(a^2 −1))∫_0 ^∞ ((1/(t^2 +1))−(1/(t^2 +a^2 )))dt =((πa)/(2(a^2 −1)))−(a/(a^2 −1)) ∫_0 ^∞ (dt/(t^2 +a^2 )) we have ∫_0 ^∞ (dt/(t^2 +a^2 )) =_(t=aα) ∫_0 ^∞ ((adα)/(a^2 (1+α^2 ))) =(1/a)(π/2) ⇒ f^′ (a) =((πa)/(2(a^2 −1)))−(/(a^2 −1))×(π/2) =(π/(2(a^2 −1)))(a−1) =(π/(2(a+1))) ⇒f(a) =(π/2)ln(a+1) +C f(0) =0 =C ⇒f(a) =(π/2)ln(a+1) and ∫_0 ^(π/2) ((arctan((√2)tanx))/(tanx))dx =f((√2)) =(π/2)ln(1+(√2))
$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{arctan}\left({atanx}\right)}{{tanx}}{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{tanx}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {tan}^{\mathrm{2}} {x}\right){tanx}}{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{1}+{a}^{\mathrm{2}} {tan}^{\mathrm{2}} {x}} \\ $$$$=_{{atanx}\:={t}} \:\:\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{{a}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}{dt}\:={a}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)} \\ $$$$=\frac{{a}}{{a}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right){dt}\:\:=\frac{\pi{a}}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{{a}}{{a}^{\mathrm{2}} −\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:=_{{t}={a}\alpha} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ad}\alpha}{{a}^{\mathrm{2}} \left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{a}}\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\frac{\pi{a}}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}−\frac{}{{a}^{\mathrm{2}} −\mathrm{1}}×\frac{\pi}{\mathrm{2}}\:\:=\frac{\pi}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}\left({a}−\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{2}\left({a}+\mathrm{1}\right)}\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left({a}+\mathrm{1}\right)\:+{C} \\ $$$${f}\left(\mathrm{0}\right)\:=\mathrm{0}\:={C}\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left({a}+\mathrm{1}\right)\:{and} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{arctan}\left(\sqrt{\mathrm{2}}{tanx}\right)}{{tanx}}{dx}\:={f}\left(\sqrt{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 02/Apr/20
cool
$${cool} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *