Menu Close

0-pi-2-cos-10-x-sin-12x-dx-Given-reduction-formula-cos-m-x-sin-nx-dx-I-m-n-cos-m-x-cosnx-m-n-m-m-n-I-m-1-n-1-

Tinku Tara 0 Comments
Pin




Question Number 39280 by rahul 19 last updated on 04/Jul/18
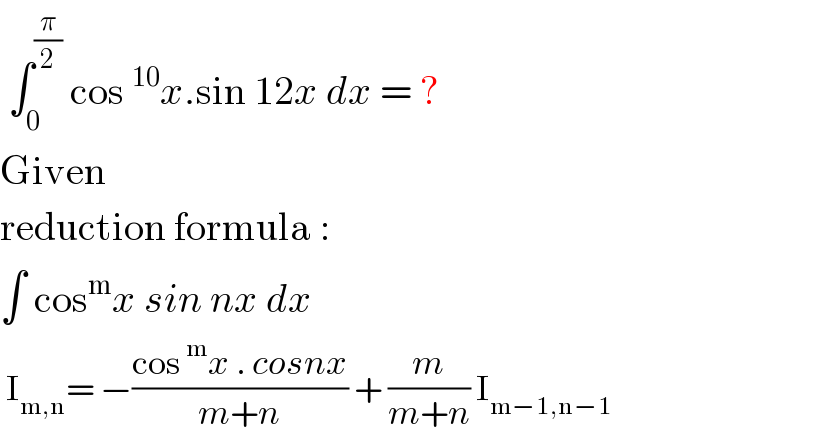
∫_0 ^(π/2) cos^(10) x.sin 12x dx = ? Given reduction formula : ∫ cos^m x sin nx dx I_(m,n) = −((cos^m x . cosnx)/(m+n)) + (m/(m+n)) I_(m−1,n−1)
$$\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\:^{\mathrm{10}} {x}.\mathrm{sin}\:\mathrm{12}{x}\:{dx}\:=\:? \\ $$$$\mathrm{Given} \\ $$$$\mathrm{reduction}\:\mathrm{formula}\:: \\ $$$$\int\:\mathrm{cos}^{\mathrm{m}} {x}\:{sin}\:{nx}\:{dx}\: \\ $$$$\:\mathrm{I}_{\mathrm{m},\mathrm{n}} =\:−\frac{\mathrm{cos}\:^{\mathrm{m}} {x}\:.\:{cosnx}}{{m}+{n}}\:+\:\frac{{m}}{{m}+{n}}\:\mathrm{I}_{\mathrm{m}−\mathrm{1},\mathrm{n}−\mathrm{1}} \\ $$
Commented by rahul 19 last updated on 04/Jul/18
Someone pls do by reduction formulae given. ?????????
Answered by MJS last updated on 04/Jul/18
cos^(10 ) x sin 12x= =sin 12x ((1/(512))cos 10x +(5/(256))cos 8x +((45)/(512))cos 6x +((15)/(64))cos 4x +((105)/(256))cos 2x +((63)/(256)))= [sin ax cos bx =(1/2)sin((a−b)x)+(1/2)sin((a+b)x)] =(1/(1024))sin 22x +(5/(512))sin 20x +((45)/(1024))sin 18x +((15)/(128))sin 16x +((105)/(512))sin 14x +((63)/(256))sin 12x +((105)/(512))sin 10x +((15)/(128))sin 8x +((45)/(1024))sin 6x +(5/(512))sin 4x +(1/(1024))sin 2x= =Σ_(k=0) ^(10) ( (((10)),(k) )/2^(10) )sin((22−2k)x) ∫(Σ_(k=0) ^(10) ( (((10)),(k) )/2^(10) )sin((22−2k)x))dx= =−Σ_(k=0) ^(10) ( (((10)),(k) )/(2^(10) (22−2k)))cos((22−2k)x)=(1/(11))
$$\mathrm{cos}^{\mathrm{10}\:} \:{x}\:\mathrm{sin}\:\mathrm{12}{x}= \\ $$$$=\mathrm{sin}\:\mathrm{12}{x}\:\left(\frac{\mathrm{1}}{\mathrm{512}}\mathrm{cos}\:\mathrm{10}{x}\:+\frac{\mathrm{5}}{\mathrm{256}}\mathrm{cos}\:\mathrm{8}{x}\:+\frac{\mathrm{45}}{\mathrm{512}}\mathrm{cos}\:\mathrm{6}{x}\:+\frac{\mathrm{15}}{\mathrm{64}}\mathrm{cos}\:\mathrm{4}{x}\:+\frac{\mathrm{105}}{\mathrm{256}}\mathrm{cos}\:\mathrm{2}{x}\:+\frac{\mathrm{63}}{\mathrm{256}}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:{ax}\:\mathrm{cos}\:{bx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\left({a}−{b}\right){x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\left({a}+{b}\right){x}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{1024}}\mathrm{sin}\:\mathrm{22}{x}\:+\frac{\mathrm{5}}{\mathrm{512}}\mathrm{sin}\:\mathrm{20}{x}\:+\frac{\mathrm{45}}{\mathrm{1024}}\mathrm{sin}\:\mathrm{18}{x}\:+\frac{\mathrm{15}}{\mathrm{128}}\mathrm{sin}\:\mathrm{16}{x}\:+\frac{\mathrm{105}}{\mathrm{512}}\mathrm{sin}\:\mathrm{14}{x}\:+\frac{\mathrm{63}}{\mathrm{256}}\mathrm{sin}\:\mathrm{12}{x}\:+\frac{\mathrm{105}}{\mathrm{512}}\mathrm{sin}\:\mathrm{10}{x}\:+\frac{\mathrm{15}}{\mathrm{128}}\mathrm{sin}\:\mathrm{8}{x}\:+\frac{\mathrm{45}}{\mathrm{1024}}\mathrm{sin}\:\mathrm{6}{x}\:+\frac{\mathrm{5}}{\mathrm{512}}\mathrm{sin}\:\mathrm{4}{x}\:+\frac{\mathrm{1}}{\mathrm{1024}}\mathrm{sin}\:\mathrm{2}{x}= \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\frac{\begin{pmatrix}{\mathrm{10}}\\{{k}}\end{pmatrix}}{\mathrm{2}^{\mathrm{10}} }\mathrm{sin}\left(\left(\mathrm{22}−\mathrm{2}{k}\right){x}\right) \\ $$$$\int\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\frac{\begin{pmatrix}{\mathrm{10}}\\{{k}}\end{pmatrix}}{\mathrm{2}^{\mathrm{10}} }\mathrm{sin}\left(\left(\mathrm{22}−\mathrm{2}{k}\right){x}\right)\right){dx}= \\ $$$$=−\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}\frac{\begin{pmatrix}{\mathrm{10}}\\{{k}}\end{pmatrix}}{\mathrm{2}^{\mathrm{10}} \left(\mathrm{22}−\mathrm{2}{k}\right)}\mathrm{cos}\left(\left(\mathrm{22}−\mathrm{2k}\right){x}\right)=\frac{\mathrm{1}}{\mathrm{11}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jul/18
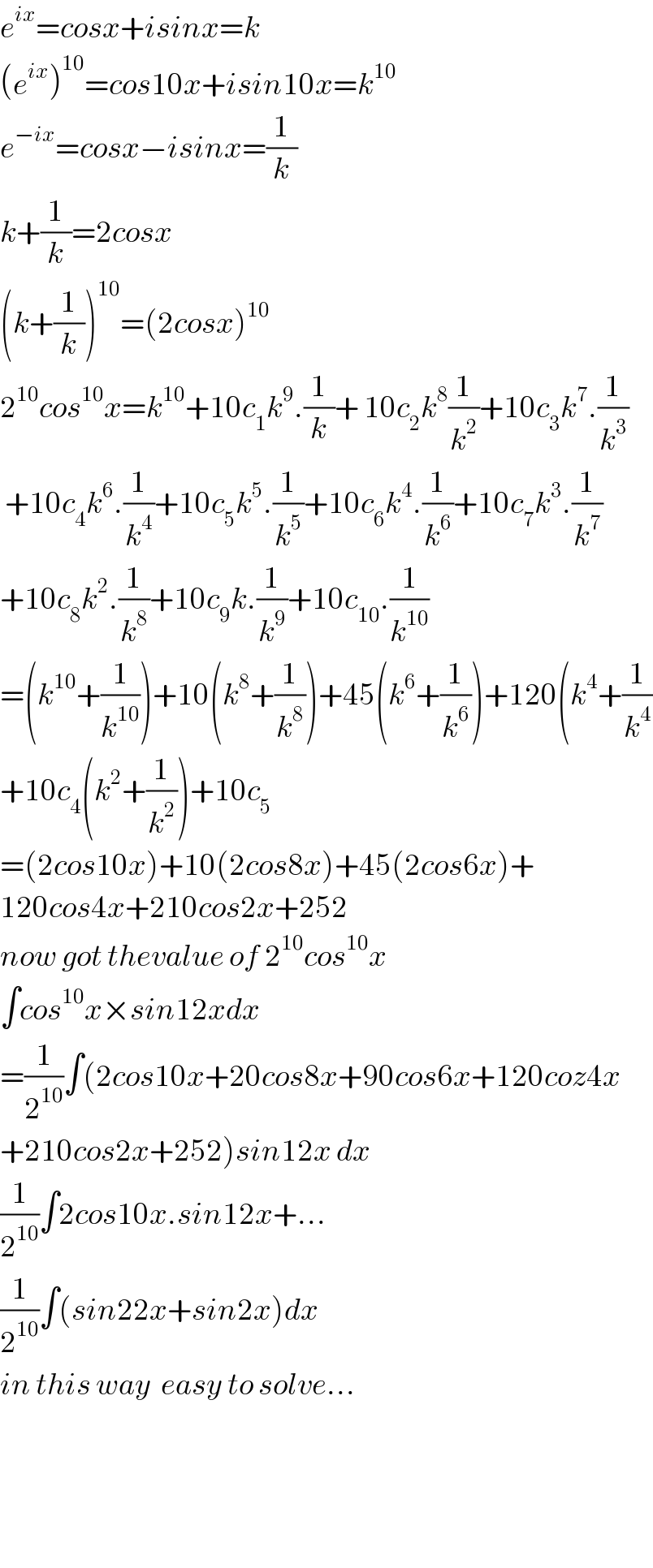
e^(ix) =cosx+isinx=k (e^(ix) )^(10) =cos10x+isin10x=k^(10) e^(−ix) =cosx−isinx=(1/k) k+(1/k)=2cosx (k+(1/k))^(10) =(2cosx)^(10) 2^(10) cos^(10) x=k^(10) +10c_1 k^9 .(1/k)+ 10c_2 k^8 (1/k^2 )+10c_3 k^7 .(1/k^3 ) +10c_4 k^6 .(1/k^4 )+10c_5 k^5 .(1/k^5 )+10c_6 k^4 .(1/k^6 )+10c_7 k^3 .(1/k^7 ) +10c_8 k^2 .(1/k^8 )+10c_9 k.(1/k^9 )+10c_(10) .(1/k^(10) ) =(k^(10) +(1/k^(10) ))+10(k^8 +(1/k^8 ))+45(k^6 +(1/k^6 ))+120(k^4 +(1/k^4 ) +10c_4 (k^2 +(1/k^2 ))+10c_5 =(2cos10x)+10(2cos8x)+45(2cos6x)+ 120cos4x+210cos2x+252 now got thevalue of 2^(10) cos^(10) x ∫cos^(10) x×sin12xdx =(1/2^(10) )∫(2cos10x+20cos8x+90cos6x+120coz4x +210cos2x+252)sin12x dx (1/2^(10) )∫2cos10x.sin12x+... (1/2^(10) )∫(sin22x+sin2x)dx in this way easy to solve...
$${e}^{{ix}} ={cosx}+{isinx}={k} \\ $$$$\left({e}^{{ix}} \right)^{\mathrm{10}} ={cos}\mathrm{10}{x}+{isin}\mathrm{10}{x}={k}^{\mathrm{10}} \\ $$$${e}^{−{ix}} ={cosx}−{isinx}=\frac{\mathrm{1}}{{k}} \\ $$$${k}+\frac{\mathrm{1}}{{k}}=\mathrm{2}{cosx} \\ $$$$\left({k}+\frac{\mathrm{1}}{{k}}\right)^{\mathrm{10}} =\left(\mathrm{2}{cosx}\right)^{\mathrm{10}} \\ $$$$\mathrm{2}^{\mathrm{10}} {cos}^{\mathrm{10}} {x}={k}^{\mathrm{10}} +\mathrm{10}{c}_{\mathrm{1}} {k}^{\mathrm{9}} .\frac{\mathrm{1}}{{k}}+\:\mathrm{10}{c}_{\mathrm{2}} {k}^{\mathrm{8}} \frac{\mathrm{1}}{{k}^{\mathrm{2}} }+\mathrm{10}{c}_{\mathrm{3}} {k}^{\mathrm{7}} .\frac{\mathrm{1}}{{k}^{\mathrm{3}} } \\ $$$$\:+\mathrm{10}{c}_{\mathrm{4}} {k}^{\mathrm{6}} .\frac{\mathrm{1}}{{k}^{\mathrm{4}} }+\mathrm{10}{c}_{\mathrm{5}} {k}^{\mathrm{5}} .\frac{\mathrm{1}}{{k}^{\mathrm{5}} }+\mathrm{10}{c}_{\mathrm{6}} {k}^{\mathrm{4}} .\frac{\mathrm{1}}{{k}^{\mathrm{6}} }+\mathrm{10}{c}_{\mathrm{7}} {k}^{\mathrm{3}} .\frac{\mathrm{1}}{{k}^{\mathrm{7}} } \\ $$$$+\mathrm{10}{c}_{\mathrm{8}} {k}^{\mathrm{2}} .\frac{\mathrm{1}}{{k}^{\mathrm{8}} }+\mathrm{10}{c}_{\mathrm{9}} {k}.\frac{\mathrm{1}}{{k}^{\mathrm{9}} }+\mathrm{10}{c}_{\mathrm{10}} .\frac{\mathrm{1}}{{k}^{\mathrm{10}} } \\ $$$$=\left({k}^{\mathrm{10}} +\frac{\mathrm{1}}{{k}^{\mathrm{10}} }\right)+\mathrm{10}\left({k}^{\mathrm{8}} +\frac{\mathrm{1}}{{k}^{\mathrm{8}} }\right)+\mathrm{45}\left({k}^{\mathrm{6}} +\frac{\mathrm{1}}{{k}^{\mathrm{6}} }\right)+\mathrm{120}\left({k}^{\mathrm{4}} +\frac{\mathrm{1}}{{k}^{\mathrm{4}} }\right. \\ $$$$+\mathrm{10}{c}_{\mathrm{4}} \left({k}^{\mathrm{2}} +\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)+\mathrm{10}{c}_{\mathrm{5}} \\ $$$$=\left(\mathrm{2}{cos}\mathrm{10}{x}\right)+\mathrm{10}\left(\mathrm{2}{cos}\mathrm{8}{x}\right)+\mathrm{45}\left(\mathrm{2}{cos}\mathrm{6}{x}\right)+ \\ $$$$\mathrm{120}{cos}\mathrm{4}{x}+\mathrm{210}{cos}\mathrm{2}{x}+\mathrm{252} \\ $$$${now}\:{got}\:{thevalue}\:{of}\:\mathrm{2}^{\mathrm{10}} {cos}^{\mathrm{10}} {x} \\ $$$$\int{cos}^{\mathrm{10}} {x}×{sin}\mathrm{12}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\int\left(\mathrm{2}{cos}\mathrm{10}{x}+\mathrm{20}{cos}\mathrm{8}{x}+\mathrm{90}{cos}\mathrm{6}{x}+\mathrm{120}{coz}\mathrm{4}{x}\right. \\ $$$$\left.+\mathrm{210}{cos}\mathrm{2}{x}+\mathrm{252}\right){sin}\mathrm{12}{x}\:{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\int\mathrm{2}{cos}\mathrm{10}{x}.{sin}\mathrm{12}{x}+… \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }\int\left({sin}\mathrm{22}{x}+{sin}\mathrm{2}{x}\right){dx} \\ $$$${in}\:{this}\:{way}\:\:{easy}\:{to}\:{solve}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 05/Jul/18
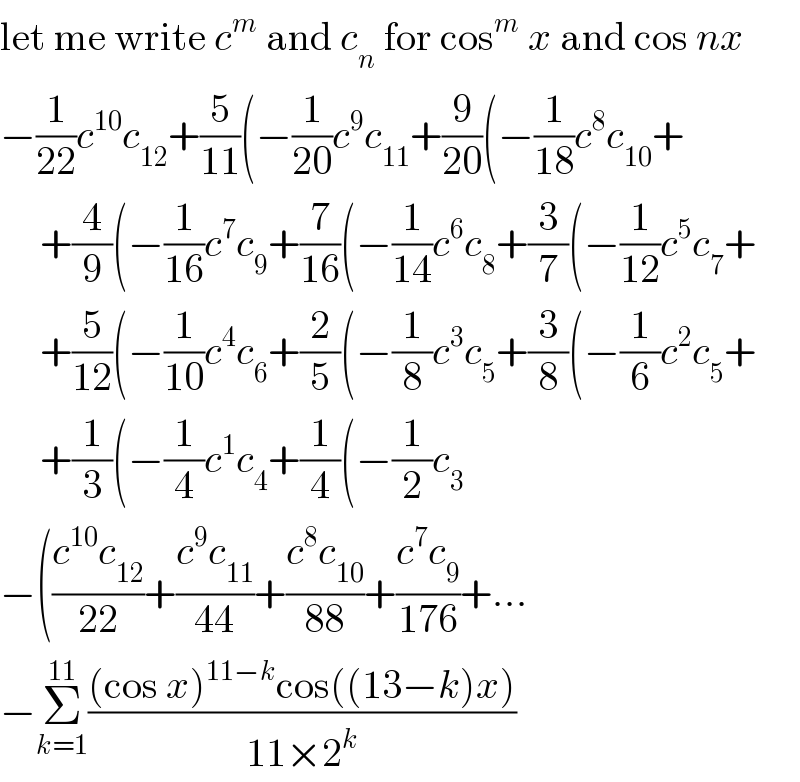
let me write c^m and c_n for cos^m x and cos nx −(1/(22))c^(10) c_(12) +(5/(11))(−(1/(20))c^9 c_(11) +(9/(20))(−(1/(18))c^8 c_(10) + +(4/9)(−(1/(16))c^7 c_9 +(7/(16))(−(1/(14))c^6 c_8 +(3/7)(−(1/(12))c^5 c_7 + +(5/(12))(−(1/(10))c^4 c_6 +(2/5)(−(1/8)c^3 c_5 +(3/8)(−(1/6)c^2 c_5 + +(1/3)(−(1/4)c^1 c_4 +(1/4)(−(1/2)c_3 −(((c^(10) c_(12) )/(22))+((c^9 c_(11) )/(44))+((c^8 c_(10) )/(88))+((c^7 c_9 )/(176))+... −Σ_(k=1) ^(11) (((cos x)^(11−k) cos((13−k)x))/(11×2^k ))
$$\mathrm{let}\:\mathrm{me}\:\mathrm{write}\:{c}^{{m}} \:\mathrm{and}\:{c}_{{n}} \:\mathrm{for}\:\mathrm{cos}^{{m}} \:{x}\:\mathrm{and}\:\mathrm{cos}\:{nx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{22}}{c}^{\mathrm{10}} {c}_{\mathrm{12}} +\frac{\mathrm{5}}{\mathrm{11}}\left(−\frac{\mathrm{1}}{\mathrm{20}}{c}^{\mathrm{9}} {c}_{\mathrm{11}} +\frac{\mathrm{9}}{\mathrm{20}}\left(−\frac{\mathrm{1}}{\mathrm{18}}{c}^{\mathrm{8}} {c}_{\mathrm{10}} +\right.\right. \\ $$$$\:\:\:\:\:+\frac{\mathrm{4}}{\mathrm{9}}\left(−\frac{\mathrm{1}}{\mathrm{16}}{c}^{\mathrm{7}} {c}_{\mathrm{9}} +\frac{\mathrm{7}}{\mathrm{16}}\left(−\frac{\mathrm{1}}{\mathrm{14}}{c}^{\mathrm{6}} {c}_{\mathrm{8}} +\frac{\mathrm{3}}{\mathrm{7}}\left(−\frac{\mathrm{1}}{\mathrm{12}}{c}^{\mathrm{5}} {c}_{\mathrm{7}} +\right.\right.\right. \\ $$$$\:\:\:\:\:+\frac{\mathrm{5}}{\mathrm{12}}\left(−\frac{\mathrm{1}}{\mathrm{10}}{c}^{\mathrm{4}} {c}_{\mathrm{6}} +\frac{\mathrm{2}}{\mathrm{5}}\left(−\frac{\mathrm{1}}{\mathrm{8}}{c}^{\mathrm{3}} {c}_{\mathrm{5}} +\frac{\mathrm{3}}{\mathrm{8}}\left(−\frac{\mathrm{1}}{\mathrm{6}}{c}^{\mathrm{2}} {c}_{\mathrm{5}} +\right.\right.\right. \\ $$$$\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{4}}{c}^{\mathrm{1}} {c}_{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{1}}{\mathrm{2}}{c}_{\mathrm{3}} \right.\right. \\ $$$$−\left(\frac{{c}^{\mathrm{10}} {c}_{\mathrm{12}} }{\mathrm{22}}+\frac{{c}^{\mathrm{9}} {c}_{\mathrm{11}} }{\mathrm{44}}+\frac{{c}^{\mathrm{8}} {c}_{\mathrm{10}} }{\mathrm{88}}+\frac{{c}^{\mathrm{7}} {c}_{\mathrm{9}} }{\mathrm{176}}+…\right. \\ $$$$−\underset{{k}=\mathrm{1}} {\overset{\mathrm{11}} {\sum}}\frac{\left(\mathrm{cos}\:{x}\right)^{\mathrm{11}−{k}} \mathrm{cos}\left(\left(\mathrm{13}−{k}\right){x}\right)}{\mathrm{11}×\mathrm{2}^{{k}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *