Question Number 153555 by mnjuly1970 last updated on 08/Sep/21
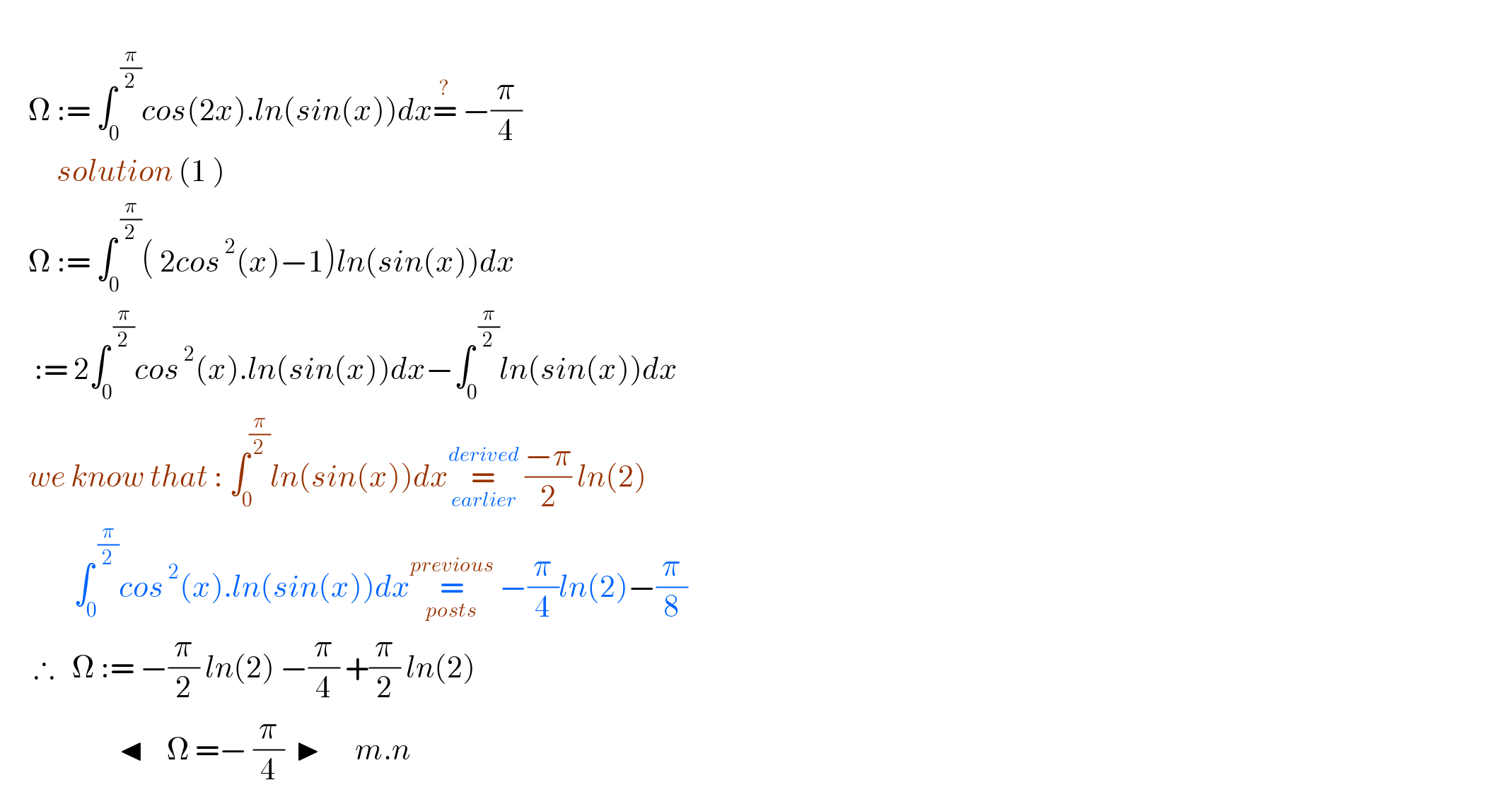
$$ \\ $$$$\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{x}\right).{ln}\left({sin}\left({x}\right)\right){dx}\overset{?} {=}\:−\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{solution}\:\left(\mathrm{1}\:\right) \\ $$$$\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left(\:\mathrm{2}{cos}^{\:\mathrm{2}} \left({x}\right)−\mathrm{1}\right){ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\::=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {cos}^{\:\mathrm{2}} \left({x}\right).{ln}\left({sin}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:{we}\:{know}\:{that}\::\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}\underset{{earlier}} {\overset{{derived}} {=}}\:\frac{−\pi}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {cos}^{\:\mathrm{2}} \left({x}\right).{ln}\left({sin}\left({x}\right)\right){dx}\underset{{posts}} {\overset{{previous}} {=}}\:−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\therefore\:\:\:\Omega\::=\:−\frac{\pi}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right)\:−\frac{\pi}{\mathrm{4}}\:+\frac{\pi}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacktriangleleft\:\:\:\:\Omega\:=−\:\frac{\pi}{\mathrm{4}}\:\:\blacktriangleright\:\:\:\:\:\:{m}.{n} \\ $$
Answered by Ar Brandon last updated on 08/Sep/21
![Ω=∫_0 ^(π/2) cos(2x)ln(sinx)dx { ((u(x)=ln(sinx))),((v′(x)=cos(2x))) :}⇒ { ((u′(x)=((cosx)/(sinx)))),((v(x)=((sin2x)/2))) :} Ω=[((ln(sinx)sin2x)/2)−∫cos^2 xdx]_0 ^(π/2) =−∫_0 ^(π/2) cos^2 xdx=−(1/2)∫_0 ^(π/2) (1+cos2x)dx =−(1/2)[x+((sin2x)/2)]_0 ^(π/2) =−(π/4)](https://www.tinkutara.com/question/Q153556.png)
$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}\left(\mathrm{2}{x}\right)\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\begin{cases}{{u}\left({x}\right)=\mathrm{ln}\left(\mathrm{sin}{x}\right)}\\{{v}'\left({x}\right)=\mathrm{cos}\left(\mathrm{2}{x}\right)}\end{cases}\Rightarrow\begin{cases}{{u}'\left({x}\right)=\frac{\mathrm{cos}{x}}{\mathrm{sin}{x}}}\\{{v}\left({x}\right)=\frac{\mathrm{sin2}{x}}{\mathrm{2}}}\end{cases} \\ $$$$\Omega=\left[\frac{\mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{sin2}{x}}{\mathrm{2}}−\int\mathrm{cos}^{\mathrm{2}} {xdx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {xdx}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos2}{x}\right){dx} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[{x}+\frac{\mathrm{sin2}{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =−\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 08/Sep/21

$$\:{very}\:{nice}\:{sir}\:{brando}\:{as}\:{always}.. \\ $$
Commented by Ar Brandon last updated on 08/Sep/21
Thanks
