Question Number 159682 by cortano last updated on 20/Nov/21
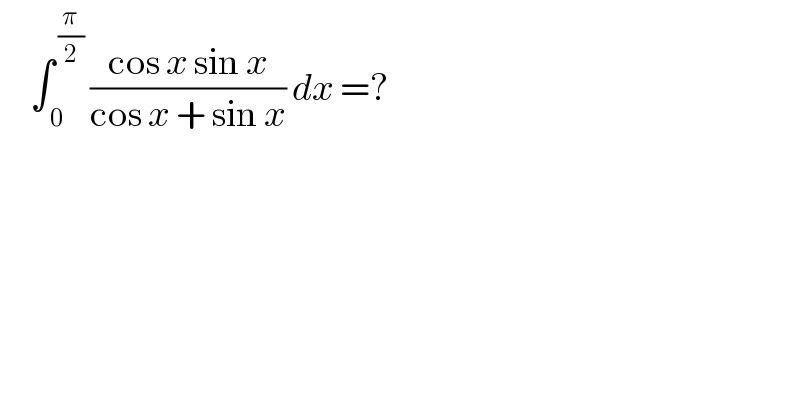
$$\:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}\:+\:\mathrm{sin}\:{x}}\:{dx}\:=?\: \\ $$
Answered by Ar Brandon last updated on 20/Nov/21
![I=∫_0 ^(π/2) ((cosxsinx)/(cosx+sinx))dx=(1/2)∫_0 ^(π/2) ((2sinxcosx)/(cosx+sinx))dx =(1/2)∫_0 ^(π/2) ((1+2sinxcosx−1)/(cosx+sinx))dx =(1/2)∫_0 ^(π/2) ((cos^2 x+2sinxcosx+sin^2 x)/(cosx+sinx))dx−(1/2)∫_0 ^(π/2) (dx/(cosx+sinx)) =(1/2)∫_0 ^(π/2) (((cosx+sinx)^2 )/(cosx+sinx))dx−(1/(2(√2)))∫_0 ^(π/2) (dx/(cos(x−(π/4)))) =(1/2)[sinx−cosx]_0 ^(π/2) −(1/(2(√2)))[ln∣sec(x−(π/4))+tan(x−(π/4))∣]_0 ^(π/2) =1−(1/(2(√2)))ln((((√2)+1)/( (√2)−1)))](https://www.tinkutara.com/question/Q159685.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}{x}\mathrm{sin}{x}}{\mathrm{cos}{x}+\mathrm{sin}{x}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2sin}{x}\mathrm{cos}{x}}{\mathrm{cos}{x}+\mathrm{sin}{x}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{2sin}{x}\mathrm{cos}{x}−\mathrm{1}}{\mathrm{cos}{x}+\mathrm{sin}{x}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{2sin}{x}\mathrm{cos}{x}+\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{cos}{x}+\mathrm{sin}{x}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{cos}{x}+\mathrm{sin}{x}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{cos}{x}+\mathrm{sin}{x}\right)^{\mathrm{2}} }{\mathrm{cos}{x}+\mathrm{sin}{x}}{dx}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{sin}{x}−\mathrm{cos}{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\mathrm{sec}\left({x}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left({x}−\frac{\pi}{\mathrm{4}}\right)\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$
Commented by cortano last updated on 20/Nov/21

$${yes}\:{nice} \\ $$
Answered by chhaythean last updated on 20/Nov/21
![Ω=∫_0 ^(π/2) ((sinxcosx)/(sinx+cosx))dx 2Ω=∫_0 ^(π/2) ((2sinxcosx)/(sinx+cosx))dx 2Ω=∫_0 ^(π/2) (((sinx+cosx)^2 )/(sinx+cosx))dx−∫_0 ^(π/2) (1/(sinx+cosx))dx 2Ω=[−cosx+sinx]_0 ^(π/2) −Ω_1 2Ω=2−Ω_1 For Ω_1 Ω_1 =∫_0 ^(π/2) (1/(sinx+cosx))dx =(1/( (√2)))∫_0 ^(π/2) (1/(sin(x+(π/4))))dx =(1/( (√2)))∫_0 ^(π/2) csc(x+(π/4))dx =(1/( (√2)))[ln∣tan((x/2)+(π/8))∣]_0 ^(π/2) =(1/( (√2)))[ln∣tan(((3π)/8))∣−ln∣tan(π/8)∣] =(1/( (√2)))[ln∣(((√2)+1)/( (√2)−1))∣] We get: 2Ω=2−(1/( (√2)))[ln∣(((√2)+1)/( (√2)−1))∣] So determinant (((Ω=1−(1/(2(√2)))ln∣(((√2)+1)/( (√2)−1))∣)))](https://www.tinkutara.com/question/Q159695.png)
$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinxcosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$\mathrm{2}\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2sinxcosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$\mathrm{2}\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{sinx}+\mathrm{cosx}\right)^{\mathrm{2}} }{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$\mathrm{2}\Omega=\left[−\mathrm{cosx}+\mathrm{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\Omega_{\mathrm{1}} \\ $$$$\mathrm{2}\Omega=\mathrm{2}−\Omega_{\mathrm{1}} \\ $$$$\mathrm{For}\:\Omega_{\mathrm{1}} \\ $$$$\Omega_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{csc}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\mid−\mathrm{ln}\mid\mathrm{tan}\frac{\pi}{\mathrm{8}}\mid\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid\right] \\ $$$$\mathrm{We}\:\mathrm{get}:\:\mathrm{2}\Omega=\mathrm{2}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid\right] \\ $$$$\mathrm{So}\:\begin{array}{|c|}{\Omega=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid}\\\hline\end{array} \\ $$
Answered by mathmax by abdo last updated on 20/Nov/21
![I=(1/2)∫_0 ^(π/2) ((1+2cosx sinx −1)/((cosx+sinx)))dx =(1/2)∫_0 ^(π/2) (((cosx+sinx)^2 −1)/(cosx+sinx))dx =(1/2)∫_0 ^(π/2) (cosx +sinx)dx−(1/2)∫_0 ^(π/2) (dx/(cosx +sinx)) but ∫_0 ^(π/2) (cosx +sinx)dx=[sinx−cosx]_0 ^(π/2) =1−(−1)=2 ∫_0 ^(π/2) (dx/(cosx +sinx))=_(tan((x/2))=t) ∫_0 ^1 ((2dt)/((1+t^2 )(((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 ))))) =∫_0 ^1 ((2dt)/(1−t^2 +2t))=−2∫_0 ^1 (dt/(t^2 −2t−1))=−2∫_0 ^(1 ) (dt/((t−1)^2 −2)) =−2∫_0 ^1 (dt/((t−1−(√2))(t−1+(√2))))=−(2/(2(√2)))∫_0 ^1 ((1/(t−1−(√2)))−(1/(t−1+(√2))))dt =−(1/( (√2)))[ln∣((t−1−(√2))/(t−1+(√2)))∣]_0 ^1 =−(1/( (√2))){−ln((((√2)+1)/( (√2)−1)))} =(1/( (√2)))ln((((√2)+1)/( (√2)−1))) ⇒ I=1−(1/(2(√2)))ln((((√2)+1)/( (√2)−1)))](https://www.tinkutara.com/question/Q159743.png)
$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{2cosx}\:\mathrm{sinx}\:−\mathrm{1}}{\left(\mathrm{cosx}+\mathrm{sinx}\right)}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{cosx}+\mathrm{sinx}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{cosx}+\mathrm{sinx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cosx}\:+\mathrm{sinx}\right)\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{cosx}\:+\mathrm{sinx}} \\ $$$$\mathrm{but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cosx}\:+\mathrm{sinx}\right)\mathrm{dx}=\left[\mathrm{sinx}−\mathrm{cosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1}−\left(−\mathrm{1}\right)=\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{cosx}\:+\mathrm{sinx}}=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}}=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}−\mathrm{1}}=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left(\mathrm{t}−\mathrm{1}+\sqrt{\mathrm{2}}\right)}=−\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}+\sqrt{\mathrm{2}}}\right)\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{t}−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{−\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\right\}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$ \\ $$$$ \\ $$
