Question Number 174192 by Best1 last updated on 26/Jul/22
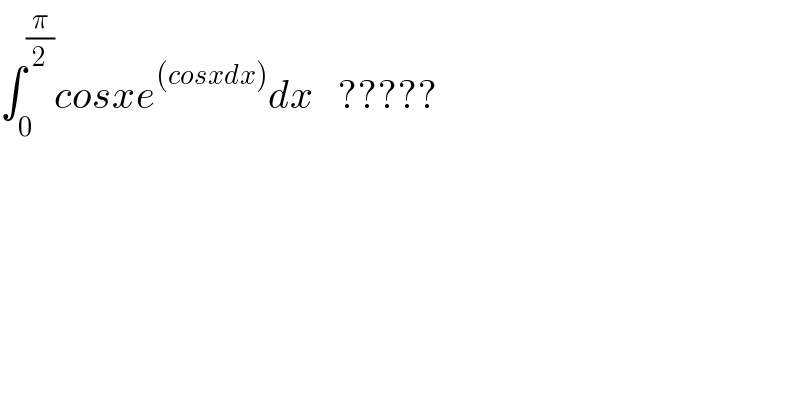
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosxe}^{\left({cosxdx}\right)} {dx}\:\:\:????? \\ $$
Commented by Best1 last updated on 27/Jul/22

$${help} \\ $$
Commented by mr W last updated on 27/Jul/22

$${the}\:{question}\:{is}\:{non}−{sense}. \\ $$$${cosxe}^{\left({cosxdx}\right)} \:{is}\:{not}\:{a}\:{valid}\:{function}! \\ $$
Commented by Best1 last updated on 28/Jul/22
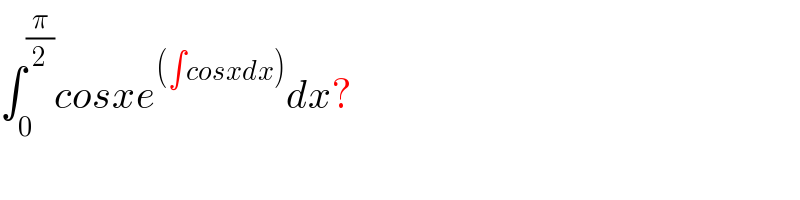
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosxe}^{\left(\int{cosxdx}\right)} {dx}? \\ $$
Commented by Best1 last updated on 28/Jul/22

$$ \\ $$
Commented by mr W last updated on 28/Jul/22
![∫_0 ^(π/2) cosxe^((∫cosxdx)) dx =∫_0 ^(π/2) cosxe^((sin x+C)) dx =∫_0 ^(π/2) e^((sin x+C)) d(sin x+C) =[e^((sin x+C)) ]_0 ^(π/2) =e^(1+C) −e^C =(e−1)e^C](https://www.tinkutara.com/question/Q174256.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosxe}^{\left(\int{cosxdx}\right)} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosxe}^{\left(\mathrm{sin}\:{x}+{C}\right)} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{\left(\mathrm{sin}\:{x}+{C}\right)} {d}\left(\mathrm{sin}\:{x}+{C}\right) \\ $$$$=\left[{e}^{\left(\mathrm{sin}\:{x}+{C}\right)} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$={e}^{\mathrm{1}+{C}} −{e}^{{C}} \\ $$$$=\left({e}−\mathrm{1}\right){e}^{{C}} \\ $$
