Menu Close

0-pi-2-dx-1-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 95848 by john santu last updated on 28/May/20
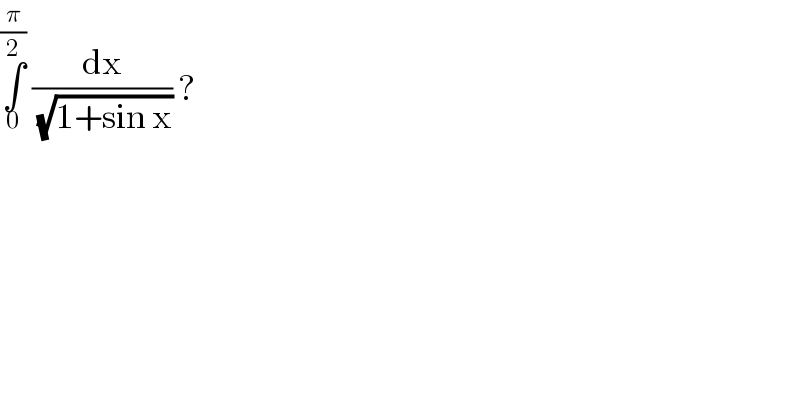
∫_0 ^(π/2) (dx/( (√(1+sin x)))) ?
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}\:?\: \\ $$
Answered by bobhans last updated on 28/May/20
∫_0 ^(π/2) (dx/( (√((sin (x/2)+cos (x/2))^2 )))) = ∫_0 ^(π/2) (dx/( (√2) cos ((x/2)−(π/4)))) set (x/2)−(π/4) = t ⇒ dx = 2 dt ∫_(−(π/4)) ^0 ((2 dt)/( (√(2 )) cos t)) =(√2) [ln ∣sec t + tan t ∣] _(−(π/4))^( 0) =(√2) ln ∣((1+sin t)/(cos t))∣ _(−(π/4)) ^0 = (√2) (0−ln((√2)−1) = (√2) ln((1/( (√2)−1))) = (√2) ln ((√2)+1)
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{dx}}{\:\sqrt{\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)}\: \\ $$$$\mathrm{set}\:\frac{\mathrm{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\:\mathrm{t}\:\Rightarrow\:\mathrm{dx}\:=\:\mathrm{2}\:\mathrm{dt}\: \\ $$$$\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\mathrm{0}} {\int}}\frac{\mathrm{2}\:\mathrm{dt}}{\:\sqrt{\mathrm{2}\:}\:\mathrm{cos}\:\mathrm{t}}\:=\sqrt{\mathrm{2}}\:\:\left[\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{t}\:+\:\mathrm{tan}\:\mathrm{t}\:\mid\right]\:_{−\frac{\pi}{\mathrm{4}}} ^{\:\:\mathrm{0}} \\ $$$$=\sqrt{\mathrm{2}}\:\:\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{t}}{\mathrm{cos}\:\mathrm{t}}\mid\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\mathrm{0}} {\:}}\:=\:\sqrt{\mathrm{2}}\:\left(\mathrm{0}−\mathrm{ln}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right. \\ $$$$=\:\sqrt{\mathrm{2}}\:\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\:=\:\sqrt{\mathrm{2}}\:\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\:\: \\ $$
Answered by john santu last updated on 28/May/20
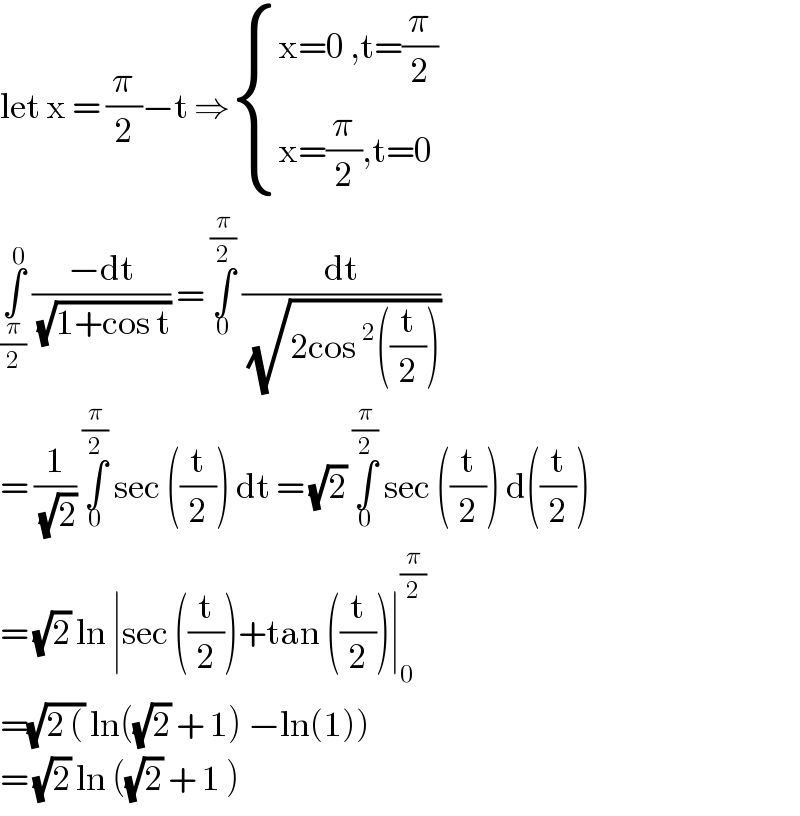
let x = (π/2)−t ⇒ { ((x=0 ,t=(π/2))),((x=(π/2),t=0)) :} ∫_(π/2) ^0 ((−dt)/( (√(1+cos t)))) = ∫_0 ^(π/2) (dt/( (√(2cos^2 ((t/2)))))) = (1/( (√2))) ∫_0 ^(π/2) sec ((t/2)) dt = (√2) ∫_0 ^(π/2) sec ((t/2)) d((t/2)) = (√2) ln ∣sec ((t/2))+tan ((t/2))∣_0 ^(π/2) =(√(2 ()) ln((√2) + 1) −ln(1)) = (√2) ln ((√2) + 1 )
$$\mathrm{let}\:\mathrm{x}\:=\:\frac{\pi}{\mathrm{2}}−\mathrm{t}\:\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{0}\:,\mathrm{t}=\frac{\pi}{\mathrm{2}}}\\{\mathrm{x}=\frac{\pi}{\mathrm{2}},\mathrm{t}=\mathrm{0}}\end{cases} \\ $$$$\underset{\frac{\pi}{\mathrm{2}}} {\overset{\mathrm{0}} {\int}}\:\frac{−\mathrm{dt}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:\mathrm{t}}}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)}}\: \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{sec}\:\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\:\mathrm{dt}\:=\:\sqrt{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{sec}\:\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\:\mathrm{d}\left(\frac{\mathrm{t}}{\mathrm{2}}\right) \\ $$$$=\:\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mid\mathrm{sec}\:\left(\frac{\mathrm{t}}{\mathrm{2}}\right)+\mathrm{tan}\:\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\left.=\sqrt{\mathrm{2}\:\left(\right.}\:\mathrm{ln}\left(\sqrt{\mathrm{2}}\:+\:\mathrm{1}\right)\:−\mathrm{ln}\left(\mathrm{1}\right)\right) \\ $$$$=\:\sqrt{\mathrm{2}}\:\mathrm{ln}\:\left(\sqrt{\mathrm{2}}\:+\:\mathrm{1}\:\right)\: \\ $$
Answered by 1549442205 last updated on 28/May/20
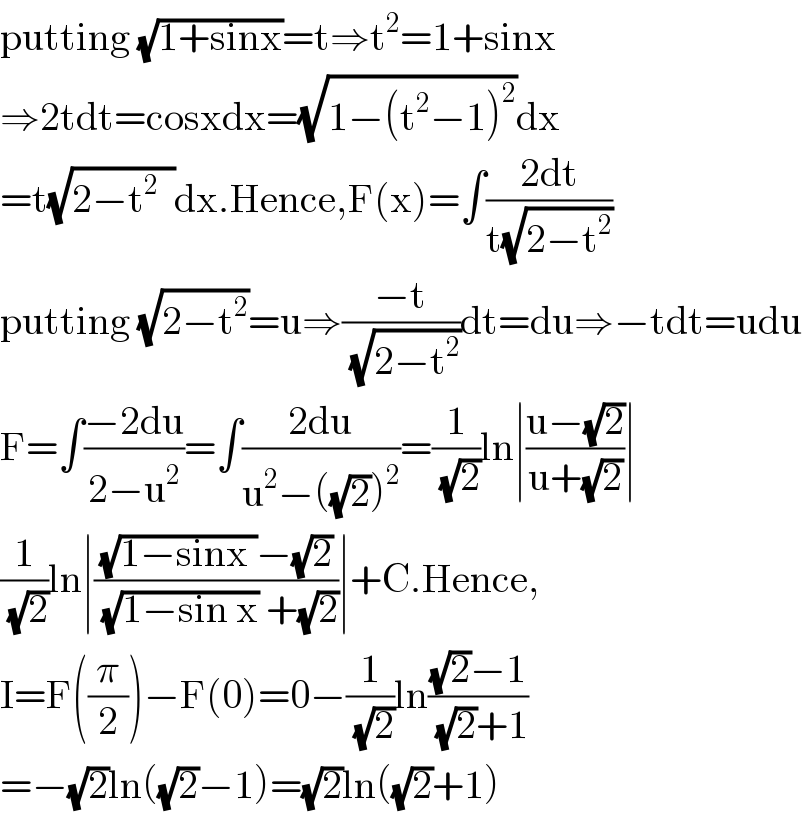
putting (√(1+sinx))=t⇒t^2 =1+sinx ⇒2tdt=cosxdx=(√(1−(t^2 −1)^2 ))dx =t(√(2−t^2 ))dx.Hence,F(x)=∫((2dt)/(t(√(2−t^2 )))) putting (√(2−t^2 ))=u⇒((−t)/( (√(2−t^2 ))))dt=du⇒−tdt=udu F=∫((−2du)/(2−u^2 ))=∫((2du)/(u^2 −((√2))^2 ))=(1/( (√2)))ln∣((u−(√2))/(u+(√2)))∣ (1/( (√2)))ln∣(((√(1−sinx ))−(√2))/( (√(1−sin x)) +(√2)))∣+C.Hence, I=F((π/2))−F(0)=0−(1/( (√2)))ln(((√2)−1)/( (√2)+1)) =−(√2)ln((√2)−1)=(√2)ln((√2)+1)
$$\mathrm{putting}\:\sqrt{\mathrm{1}+\mathrm{sinx}}=\mathrm{t}\Rightarrow\mathrm{t}^{\mathrm{2}} =\mathrm{1}+\mathrm{sinx} \\ $$$$\Rightarrow\mathrm{2tdt}=\mathrm{cosxdx}=\sqrt{\mathrm{1}−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{t}\sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} \:\:}\mathrm{dx}.\mathrm{Hence},\mathrm{F}\left(\mathrm{x}\right)=\int\frac{\mathrm{2dt}}{\mathrm{t}\sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} }} \\ $$$$\mathrm{putting}\:\sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} }=\mathrm{u}\Rightarrow\frac{−\mathrm{t}}{\:\sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\mathrm{du}\Rightarrow−\mathrm{tdt}=\mathrm{udu} \\ $$$$\mathrm{F}=\int\frac{−\mathrm{2du}}{\mathrm{2}−\mathrm{u}^{\mathrm{2}} }=\int\frac{\mathrm{2du}}{\mathrm{u}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{u}−\sqrt{\mathrm{2}}}{\mathrm{u}+\sqrt{\mathrm{2}}}\mid \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{1}−\mathrm{sinx}\:}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\:+\sqrt{\mathrm{2}}}\mid+\mathrm{C}.\mathrm{Hence}, \\ $$$$\mathrm{I}=\mathrm{F}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{F}\left(\mathrm{0}\right)=\mathrm{0}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}} \\ $$$$=−\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\sqrt{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$
Commented by john santu last updated on 28/May/20
oo you change it
$$\mathrm{oo}\:\mathrm{you}\:\mathrm{change}\:\mathrm{it}\: \\ $$
Answered by mathmax by abdo last updated on 28/May/20
I =∫_0 ^(π/2) (dx/( (√(1+sinx)))) ⇒I =∫_0 ^(π/2) (dx/( (√(cos^2 ((x/2))+sin^2 ((x/2)) +sin((x/2))cos((x/2)))))) =∫_0 ^(π/2) (dx/( (√((cos((x/2))+sin((x/2)))^2 )))) =∫_0 ^(π/2) (dx/(cos((x/2))+sin((x/2)))) =_((x/2)=t) ∫_0 ^(π/4) ((2dt)/(cost +sint)) =_(tan((t/2))=u) ∫_0 ^((√2)−1) ((4du)/((1+u^2 )(((1−u^2 )/(1+u^2 )) +((2u)/(1+u^2 ))))) =4 ∫_0 ^((√2)−1) (du/(1−u^2 +2u)) =−4 ∫_0 ^((√2)−1) (du/(u^2 −2u−1)) =−4 ∫_0 ^((√2)−1) (du/((u−1)^2 −2)) =−4 ∫_0 ^((√2)−1) (du/((u−1−(√2))(u−1+(√2)))) =((−4)/(2(√2)))∫_0 ^((√2)−1) {(1/(u−1−(√2)))−(1/(u−1+(√2)))}du =−(√2)[ln∣((u−1−(√2))/(u−1+(√2)))∣]_0 ^((√2)−1) =−(√2){ln∣((−2)/(2(√2)−2))∣−ln∣((1+(√2))/(−1+(√2)))∣} =−(√2){ln∣(1/(2−(√2)))∣−ln∣(((√2)+1)/( (√2)−1))∣ =(√2){ln(2−(√2))+ln((((√2)+1)/( (√2)−1)))}
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{sinx}}}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\:\sqrt{\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}\:=_{\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{2dt}}{\mathrm{cost}\:+\mathrm{sint}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{4du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:+\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}} \\ $$$$=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2u}−\mathrm{1}}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left(\mathrm{u}−\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{−\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\right\}\mathrm{du} \\ $$$$=−\sqrt{\mathrm{2}}\left[\mathrm{ln}\mid\frac{\mathrm{u}−\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:=−\sqrt{\mathrm{2}}\left\{\mathrm{ln}\mid\frac{−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}\mid−\mathrm{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right\} \\ $$$$=−\sqrt{\mathrm{2}}\left\{\mathrm{ln}\mid\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{2}}}\mid−\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid\:=\sqrt{\mathrm{2}}\left\{\mathrm{ln}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)+\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\right\}\right. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *