Question Number 114699 by bemath last updated on 20/Sep/20
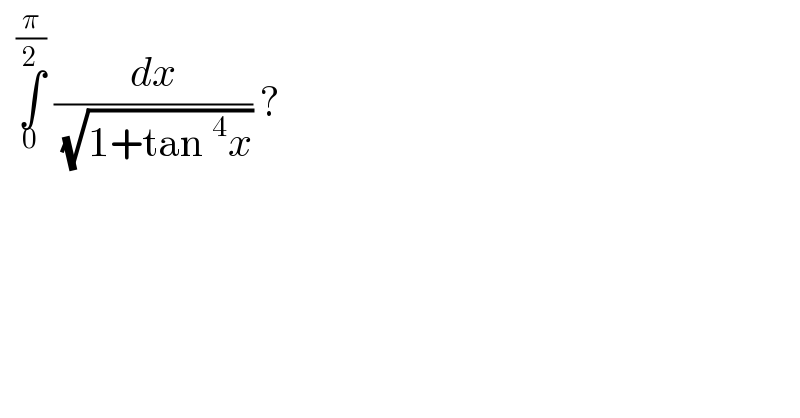
$$\:\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} {x}}}\:? \\ $$
Commented by Dwaipayan Shikari last updated on 20/Sep/20

Answered by bobhans last updated on 20/Sep/20
![replacing x = (π/2)−x I=∫_(π/2) ^0 ((−dx)/( (√(1+tan^4 ((π/2)−x))))) I=∫_0 ^(π/2) (dx/( (√(1+cot^4 x)))) = ∫_0 ^(π/2) ((tan^2 x)/( (√(tan^4 x+1))))dx 2I=∫_0 ^(π/2) ((sec^2 x)/( (√(tan^4 x+1)))) dx I=(1/2)∫_1 ^∞ (dt/( (√(t^4 +1)))) ; [ t = tan x ] set q = 1+t^4 ; t = (q−1)^(1/4) I=(1/2)∫_1 ^∞ (1/( (√q))).(1/4)(q−1)^(−(3/4)) dq I=(1/8)∫_1 ^∞ q^(−(1/2)) (q−1)^(−(3/4)) dq I= (1/( 8))∫_1 ^∞ q^(−(5/4)) (1−q^(−1) )^(−(3/4)) dq I=(1/8).((Γ^2 ((1/4)))/(Γ((1/2)))) = (1/(8(√π))).Γ^2 ((1/4))](https://www.tinkutara.com/question/Q114702.png)
$${replacing}\:{x}\:=\:\frac{\pi}{\mathrm{2}}−{x} \\ $$$${I}=\underset{\frac{\pi}{\mathrm{2}}} {\overset{\mathrm{0}} {\int}}\:\frac{−{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{cot}\:^{\mathrm{4}} {x}}}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{4}} {x}+\mathrm{1}}}{dx} \\ $$$$\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{4}} {x}+\mathrm{1}}}\:{dx}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\overset{\infty} {\int}_{\mathrm{1}} \:\frac{{dt}}{\:\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}}\:;\:\left[\:{t}\:=\:\mathrm{tan}\:{x}\:\right] \\ $$$${set}\:{q}\:=\:\mathrm{1}+{t}^{\mathrm{4}} \:;\:{t}\:=\:\left({q}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\overset{\infty} {\int}_{\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{{q}}}.\frac{\mathrm{1}}{\mathrm{4}}\left({q}−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \:{dq} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{1}} {\overset{\infty} {\int}}\:{q}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left({q}−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \:{dq} \\ $$$${I}=\:\frac{\mathrm{1}}{\:\mathrm{8}}\overset{\infty} {\int}_{\mathrm{1}} {q}^{−\frac{\mathrm{5}}{\mathrm{4}}} \left(\mathrm{1}−{q}^{−\mathrm{1}} \right)^{−\frac{\mathrm{3}}{\mathrm{4}}} {dq} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}.\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\pi}}.\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
