0-pi-2-dx-1-tan-x-

Question Number 86313 by john santu last updated on 28/Mar/20

$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}} \\ $$

Commented by john santu last updated on 28/Mar/20

((√(sin x))/( (√(sin x+cos x)))) + ((√(cos x))/( (√(sin x+cos x)))) = 1 how ?

$$\frac{\sqrt{\mathrm{sin}\:{x}}}{\:\sqrt{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}}\:+\:\frac{\sqrt{\mathrm{cos}\:{x}}}{\:\sqrt{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}}\:=\:\mathrm{1} \\ $$$${how}\:? \\ $$

Commented by john santu last updated on 28/Mar/20

(√(cos x)) + (√(sin x)) = (√(sin x+cos x)) ?

$$\sqrt{\mathrm{cos}\:{x}}\:+\:\sqrt{\mathrm{sin}\:{x}}\:=\:\sqrt{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:? \\ $$

Answered by TANMAY PANACEA. last updated on 28/Mar/20

i think... ∫_0 ^(π/2) (dx/(1+((√(sinx))/( (√(cosx))))))=∫_0 ^(π/2) ((√(cosx))/( (√(sinx)) +(√(cosx))))dx using ∫_0 ^a f(x)dx=∫_0 ^a f(a−x)dx I=∫_0 ^(π/2) ((√(cos((π/2)−x)))/( (√(sin((π/2)−x))) +(√(cos((π/2)−x)))))dx =∫_0 ^(π/2) ((√(sinx))/( (√(cosx)) +(√(sinx))))dx 2I=∫_0 ^(π/2) ((√(cosx))/( (√(sinx)) +(√(cosx))))+((√(sinx))/( (√(cosx)) +(√(sinx))))dx 2I=∫_0 ^(π/2) dx I=(π/2)×(1/2)=(π/4)

$${i}\:{think}… \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\frac{\sqrt{{sinx}}}{\:\sqrt{{cosx}}}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cosx}}}{\:\sqrt{{sinx}}\:+\sqrt{{cosx}}}{dx} \\ $$$${using}\:\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} {f}\left({a}−{x}\right){dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}}{\:\sqrt{{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:+\sqrt{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{sinx}}}{\:\sqrt{{cosx}}\:+\sqrt{{sinx}}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{cosx}}}{\:\sqrt{{sinx}}\:+\sqrt{{cosx}}}+\frac{\sqrt{{sinx}}}{\:\sqrt{{cosx}}\:+\sqrt{{sinx}}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${I}=\frac{\pi}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by jagoll last updated on 28/Mar/20

$$\mathrm{king}\:\mathrm{formula} \\ $$

Commented by TANMAY PANACEA. last updated on 28/Mar/20

$${thank}\:{you}\:{sir} \\ $$

Commented by john santu last updated on 28/Mar/20

$$\mathrm{it}\:\mathrm{does}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{wrong}\:\mathrm{sir}? \\ $$

Commented by TawaTawa1 last updated on 28/Mar/20

$$\mathrm{Sir}\:\mathrm{tanmay},\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\:\mathrm{Q86324}. \\ $$

Answered by MJS last updated on 28/Mar/20

∫(dx/( (√(1+tan x))))= [t=(√(1+tan x)) → dx=2cos^2 x (√(1+tan x))dt] =2∫(dt/(t^4 −2t^2 +2)) and now it′s easy

$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$

Commented by jagoll last updated on 28/Mar/20

= 2 ∫ (dt/((t^2 −1)^2 +1)) let t^2 −1 = tan w⇒ 2t dt = sec^2 w dw = ∫ ((sec^2 w dw)/(sec^2 w)) = w + c = tan^(−1) (t^2 −1) + c = tan^(−1) (tan (x)) + c it correct sir?

$$=\:\mathrm{2}\:\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\mathrm{let}\:\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:=\:\mathrm{tan}\:\mathrm{w}\Rightarrow\:\mathrm{2t}\:\mathrm{dt}\:=\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{w}\:\mathrm{dw} \\ $$$$=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{w}\:\mathrm{dw}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{w}}\:=\:\mathrm{w}\:+\:\mathrm{c} \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:+\:\mathrm{c} \\ $$$$=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\mathrm{x}\right)\right)\:+\:\mathrm{c} \\ $$$$\mathrm{it}\:\mathrm{correct}\:\mathrm{sir}? \\ $$

Commented by MJS last updated on 28/Mar/20

no w=arctan (t^2 −1) → dt=((t^4 −2t^3 +2)/(2t))dw ⇒ ∫(dw/( (√(1+tan w)))) so you′re back at the start

$$\mathrm{no} \\ $$$${w}=\mathrm{arctan}\:\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:\rightarrow\:{dt}=\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}}{\mathrm{2}{t}}{dw} \\ $$$$\Rightarrow\:\int\frac{{dw}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:{w}}}\:\mathrm{so}\:\mathrm{you}'\mathrm{re}\:\mathrm{back}\:\mathrm{at}\:\mathrm{the}\:\mathrm{start} \\ $$

Commented by MJS last updated on 28/Mar/20

we must decompose 2∫(dt/(t^4 −2t^2 +2))= =∫((at+b)/(t^2 −(√(2+2(√2)))t+(√2)))dt+∫((ct+d)/(t^2 +(√(2+2(√2)t+(√2)))))dt= =−((√(−1+(√2)))/2)∫((t−(√(2+2(√2))))/(t^2 −(√(2+2(√2)))t+(√2)))dt+((√(−1+(√2)))/2)∫((t+(√(2+2(√2))))/(t^2 +(√(2+(√2)))t+(√2)))dt now use formula

$$\mathrm{we}\:\mathrm{must}\:\mathrm{decompose} \\ $$$$\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}= \\ $$$$=\int\frac{{at}+{b}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}}{dt}+\int\frac{{ct}+{d}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}{t}+\sqrt{\mathrm{2}}}}{dt}= \\ $$$$=−\frac{\sqrt{−\mathrm{1}+\sqrt{\mathrm{2}}}}{\mathrm{2}}\int\frac{{t}−\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}}{dt}+\frac{\sqrt{−\mathrm{1}+\sqrt{\mathrm{2}}}}{\mathrm{2}}\int\frac{{t}+\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}}{dt} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{formula} \\ $$

Commented by jagoll last updated on 28/Mar/20

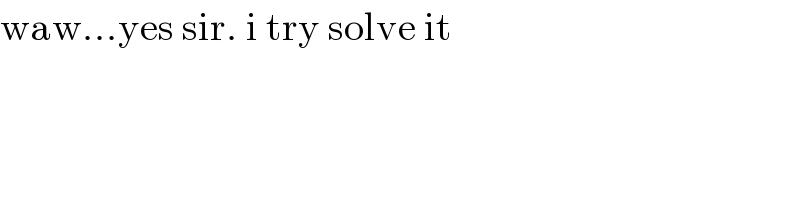
$$\mathrm{waw}…\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{try}\:\mathrm{solve}\:\mathrm{it} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply