Question Number 129185 by Dwaipayan Shikari last updated on 13/Jan/21
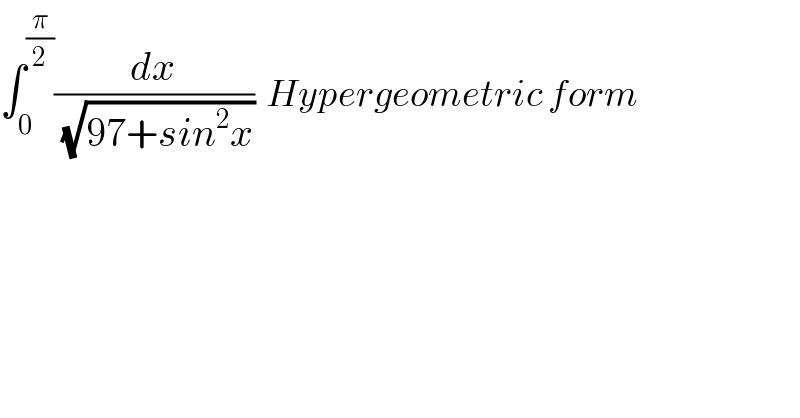
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{\mathrm{97}+{sin}^{\mathrm{2}} {x}}}\:\:{Hypergeometric}\:{form} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jan/21
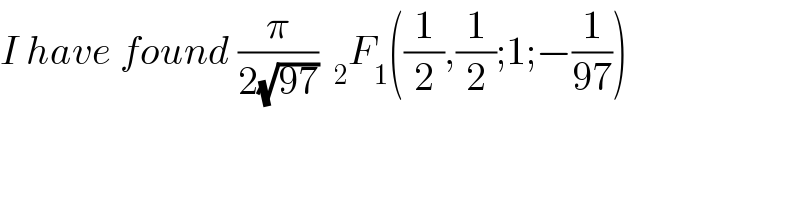
$${I}\:{have}\:{found}\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{97}}}\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{1};−\frac{\mathrm{1}}{\mathrm{97}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jan/21

$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{97}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{97}}{sin}^{\mathrm{2}} {x}\right)}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{97}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{97}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}}{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{97}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {k}^{\mathrm{2}{n}} {sin}^{\mathrm{2}{n}} {x}\:{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{97}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}{k}^{\mathrm{2}{n}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{n}} {x}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{97}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}{k}^{\mathrm{2}{n}} .\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\mathrm{1}\right)}=\frac{\sqrt{\pi}}{\:\mathrm{2}\sqrt{\mathrm{97}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} ^{\mathrm{2}} \Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{1}\right)_{{n}} {n}!}\left({k}^{\mathrm{2}} \right)^{{n}} \\ $$$$=\frac{\pi}{\:\mathrm{2}\sqrt{\mathrm{97}}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{1};{k}^{\mathrm{2}} \right)=\frac{\pi}{\mathrm{2}\:\sqrt{\mathrm{97}}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{1};−\frac{\mathrm{1}}{\mathrm{97}}\right) \\ $$$$\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \\ $$$$ \\ $$
