Question Number 154080 by iloveisrael last updated on 14/Sep/21
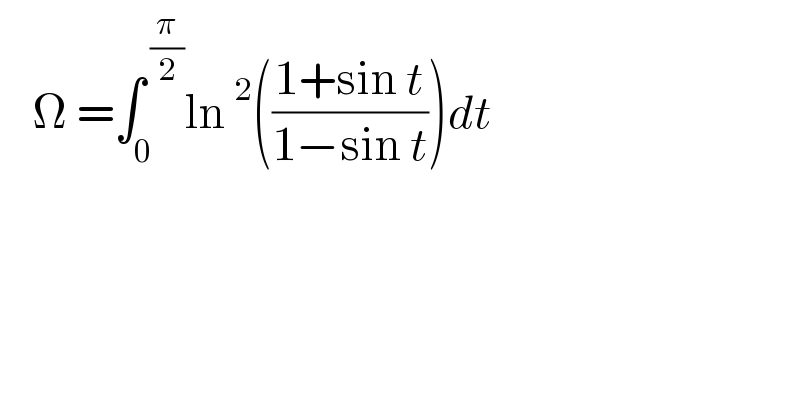
$$\:\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\:^{\mathrm{2}} \left(\frac{\mathrm{1}+\mathrm{sin}\:{t}}{\mathrm{1}−\mathrm{sin}\:{t}}\right){dt} \\ $$
Answered by mindispower last updated on 14/Sep/21
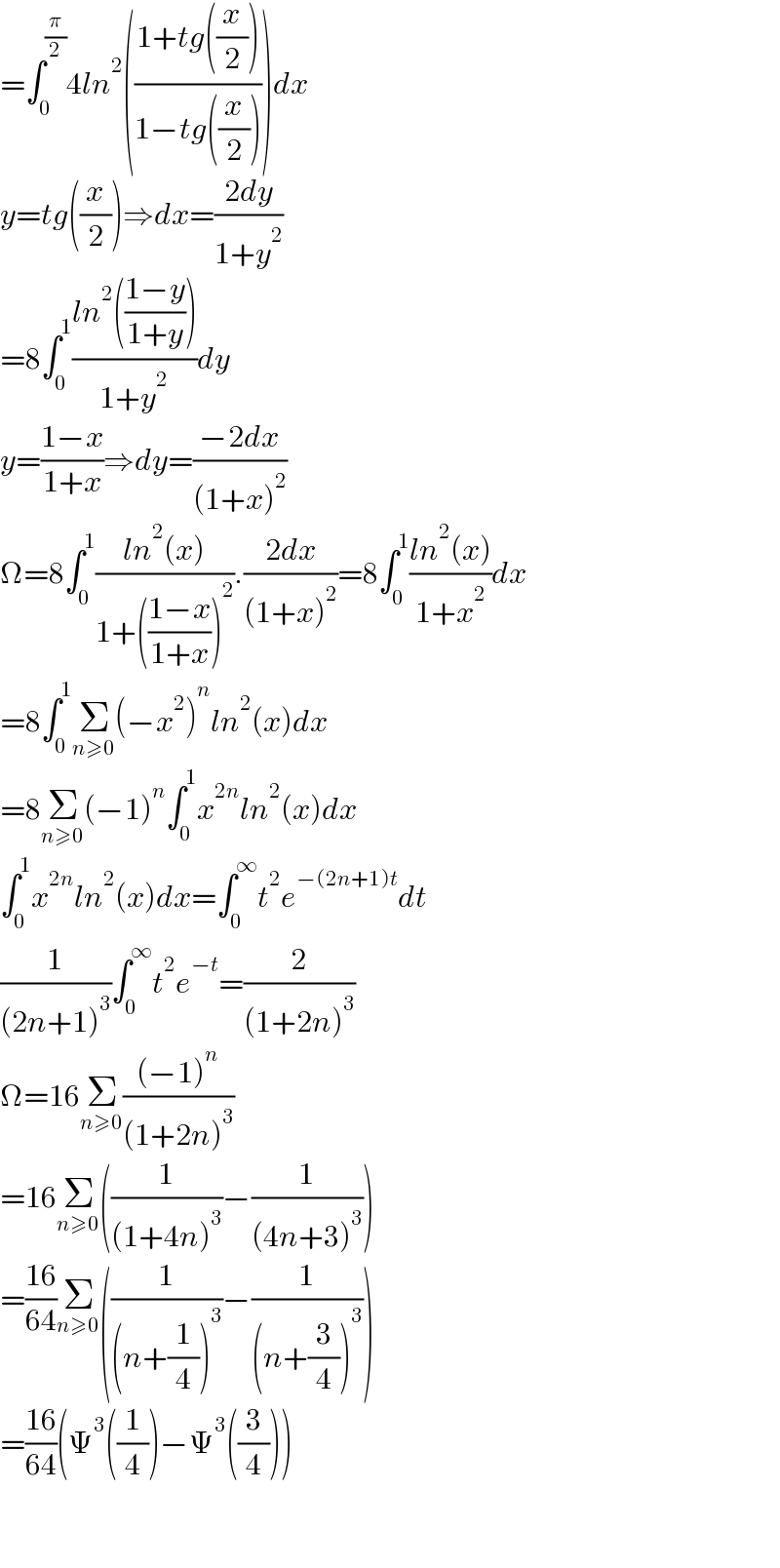
$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4}{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}+{tg}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}−{tg}\left(\frac{{x}}{\mathrm{2}}\right)}\right){dx} \\ $$$${y}={tg}\left(\frac{{x}}{\mathrm{2}}\right)\Rightarrow{dx}=\frac{\mathrm{2}{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}\right)}{\mathrm{1}+{y}^{\mathrm{2}} }{dy} \\ $$$${y}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\Rightarrow{dy}=\frac{−\mathrm{2}{dx}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} } \\ $$$$\Omega=\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{2}} }.\frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\sum}\left(−{x}^{\mathrm{2}} \right)^{{n}} {ln}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$=\mathrm{8}\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}} {ln}^{\mathrm{2}} \left({x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}} {ln}^{\mathrm{2}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}} {e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){t}} {dt} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}} {e}^{−{t}} =\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{2}{n}\right)^{\mathrm{3}} } \\ $$$$\Omega=\mathrm{16}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{1}+\mathrm{2}{n}\right)^{\mathrm{3}} } \\ $$$$=\mathrm{16}\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{4}{n}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\mathrm{3}\right)^{\mathrm{3}} }\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{64}}\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{3}} }\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{64}}\left(\Psi^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\Psi^{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right) \\ $$$$ \\ $$$$ \\ $$
