Menu Close

0-pi-2-ln-sinx-cosx-dx-by-M-A-

Tinku Tara 0 Comments
Pin




Question Number 166260 by amin96 last updated on 16/Feb/22
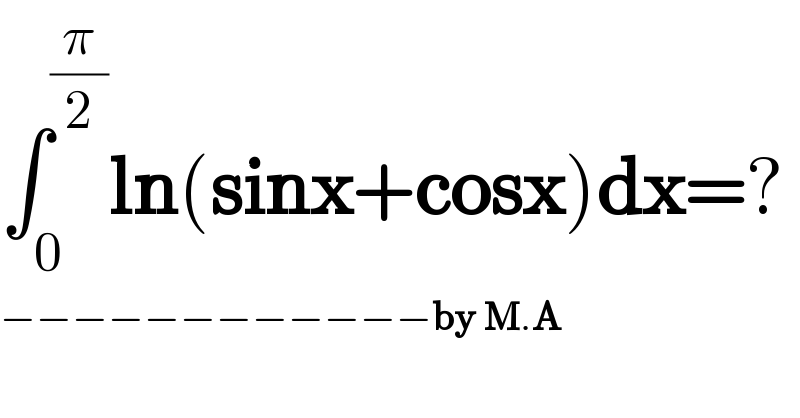
∫_0 ^(π/2) ln(sinx+cosx)dx=? −−−−−−−−−−−−by M.A
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{sinx}}+\boldsymbol{\mathrm{cosx}}\right)\boldsymbol{\mathrm{dx}}=? \\ $$$$−−−−−−−−−−−−\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{M}}.\boldsymbol{\mathrm{A}} \\ $$
Answered by Eulerian last updated on 17/Feb/22
I = ∫_0 ^( (π/2)) ln(sin x + cos x) dx = (1/2)∫_0 ^( (π/2)) ln(1+sin 2x) dx By substitution, let: z = 2x (1/2) dz = dx ∴ I = (1/4)∫_0 ^( π) ln(1+sin z) dz = (1/2)∫_0 ^( (π/2)) ln(1+sin z) dz By noticing that it somehow looks like the integral representation of Catalan′s constant, such that: G = (1/2)∫_0 ^( (π/2)) ln(sec z + tan z) dz = (1/2)∫_0 ^( (π/2)) ln(1 + sin z) − ln(cos z) dz ∴ I = (1/2)∫_0 ^( (π/2)) ln(1+sin z) − ln(cos z) + ln(cos z) dz = (1/2)∫_0 ^( (π/2)) ln(1+sin z) − ln(cos z) dz + (1/2)∫_0 ^( (π/2)) ln(cos z) dz = G + (1/2)∫_0 ^( (π/2)) ln(sin z) dz (King Rule) By adding those integrals, we get: 2I = 2G + (1/2)∫_0 ^( (π/2)) ln(sin z) dz + (1/2)∫_0 ^( (π/2)) ln(cos z) dz I = G + (1/4)∫_0 ^( (π/2)) ln(sin 2z) − ln(2) dz = G + (1/4)∫_0 ^( (π/2)) ln(sin 2z) dz − (1/4)∫_0 ^( (π/2)) ln(2) dz = G + (1/8)∫_0 ^( π) ln(sin z) dz − ((πln(2))/8) = G − ((πln(2))/8) + (1/4)∫_0 ^( (π/2)) ln(sin z) dz From what we have earlier, by comparing to what we have right now, we get: G + (1/2)∫_0 ^( (π/2)) ln(sin z) dz = G − ((πln(2))/8) + (1/4)∫_0 ^( (π/2)) ln(sin z) dz (1/2)∫_0 ^( (π/2)) ln(sin z) dz = −((πln(2))/8) + (1/4)∫_0 ^( (π/2)) ln(sin z) dz (1/2)∫_0 ^( (π/2)) ln(sin z) dz − (1/4)∫_0 ^( (π/2)) ln(sin z) dz = −((πln(2))/8) ∫_0 ^( (π/2)) ln(sin z) dz = −((πln(2))/2) Finally, we now have our answer to integral I: I = G − ((πln(2))/8) − ((1/4))∙((πln(2))/2) = G − ((πln(2))/4) Solution by: Kevin
$$\: \\ $$$$\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{cos}\:\mathrm{x}\right)\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2x}\right)\:\mathrm{dx} \\ $$$$\:\mathrm{By}\:\mathrm{substitution},\:\mathrm{let}: \\ $$$$\:\mathrm{z}\:=\:\mathrm{2x} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{dz}\:=\:\mathrm{dx} \\ $$$$\:\therefore \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\pi} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\: \\ $$$$\:\mathrm{By}\:\mathrm{noticing}\:\mathrm{that}\:\mathrm{it}\:\mathrm{somehow}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{representation}\:\mathrm{of}\:\mathrm{Catalan}'\mathrm{s} \\ $$$$\:\mathrm{constant},\:\mathrm{such}\:\mathrm{that}: \\ $$$$\:\mathrm{G}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{sec}\:\mathrm{z}\:+\:\mathrm{tan}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}\:+\:\mathrm{sin}\:\mathrm{z}\right)\:−\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\: \\ $$$$\:\therefore \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{z}\right)\:−\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:+\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{z}\right)\:−\:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:\mathrm{dz}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\:\:\:=\:\mathrm{G}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{King}}\:\boldsymbol{\mathrm{Rule}}\right) \\ $$$$\: \\ $$$$\:\mathrm{By}\:\mathrm{adding}\:\mathrm{those}\:\mathrm{integrals},\:\mathrm{we}\:\mathrm{get}: \\ $$$$\:\mathrm{2I}\:=\:\mathrm{2G}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\mathrm{I}\:=\:\mathrm{G}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{2z}\right)\:−\:\mathrm{ln}\left(\mathrm{2}\right)\:\mathrm{dz} \\ $$$$\:\:\:\:=\:\mathrm{G}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{2z}\right)\:\mathrm{dz}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}\right)\:\mathrm{dz} \\ $$$$\:\:\:\:=\:\mathrm{G}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\pi} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:−\:\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$\:\:\:\:=\:\mathrm{G}\:−\:\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\: \\ $$$$\:\mathrm{From}\:\mathrm{what}\:\mathrm{we}\:\mathrm{have}\:\mathrm{earlier},\:\mathrm{by}\:\mathrm{comparing}\:\mathrm{to}\:\mathrm{what}\:\mathrm{we}\:\mathrm{have}\:\mathrm{right}\:\mathrm{now},\:\mathrm{we}\:\mathrm{get}: \\ $$$$\:\mathrm{G}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:\mathrm{G}\:−\:\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:−\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:−\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\:\mathrm{z}\right)\:\mathrm{dz}\:=\:−\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\: \\ $$$$\:\mathrm{Finally},\:\mathrm{we}\:\mathrm{now}\:\mathrm{have}\:\mathrm{our}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{integral}\:\mathrm{I}: \\ $$$$\:\mathrm{I}\:=\:\mathrm{G}\:−\:\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:−\:\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\centerdot\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:=\:\mathrm{G}\:−\:\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\: \\ $$$$\:\boldsymbol{\mathrm{Solution}}\:\boldsymbol{\mathrm{by}}:\:\mathrm{Kevin} \\ $$
Commented by amin96 last updated on 17/Feb/22
correct answer bravo sir Kevin
$$\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{bravo}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{Kevin}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *