Menu Close

0-pi-2-log-2-tan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 123159 by Lordose last updated on 23/Nov/20
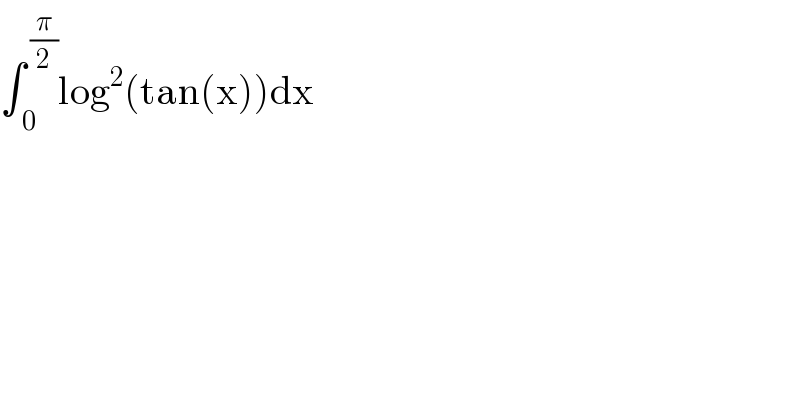
∫_( 0) ^( (π/2)) log^2 (tan(x))dx
$$\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{log}^{\mathrm{2}} \left(\mathrm{tan}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 23/Nov/20
ans:=(π^3 /8)
$${ans}:=\frac{\pi^{\mathrm{3}} }{\mathrm{8}} \\ $$
Commented by Lordose last updated on 23/Nov/20
It′s correct sir
$$\mathrm{It}'\mathrm{s}\:\mathrm{correct}\:\mathrm{sir} \\ $$
Commented by mnjuly1970 last updated on 23/Nov/20
thank you solution I=∫_0 ^( (π/2)) log^2 (tan(x))dx=^(tan(x)=y) =∫_0 ^( ∞) log^2 (y)(dy/(1+y^2 ))=^(y^2 =t) (1/8)∫_0 ^( ∞) ((t^((−1)/2) log^2 (t))/(1+t)) dt I(a) =∫_0 ^( ∞) (t^(((−1)/2)+a) /(1+t))dt goal :: I=(1/8)I ′′(0) but : I(a)=β((1/2)+a,(1/2)−a) =Γ((1/2)+a)Γ((1/2)−a) =_(reflection formula) ^(euler) (π/(sin((π/2)+πa)))=(π/(cos(πa))) I ′(a)=((π^2 sin(πa))/(cos^2 (πa))) I ′′(a)=π^2 (((πcos^3 (πa)+2πsin^2 (πa)cos(πa))/(cos^4 (πa))))∣_(a=0) I ′′(0)=π^3 ⇒ I=(π^3 /8) ✓✓
$${thank}\:{you} \\ $$$${solution} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {log}^{\mathrm{2}} \left({tan}\left({x}\right)\right){dx}\overset{{tan}\left({x}\right)={y}} {=} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\:\infty} {log}^{\mathrm{2}} \left({y}\right)\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }\overset{{y}^{\mathrm{2}} ={t}} {=}\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\infty} \:\frac{{t}^{\frac{−\mathrm{1}}{\mathrm{2}}} {log}^{\mathrm{2}} \left({t}\right)}{\mathrm{1}+{t}}\:{dt} \\ $$$$ \\ $$$$\:{I}\left({a}\right)\:=\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\frac{−\mathrm{1}}{\mathrm{2}}+{a}} }{\mathrm{1}+{t}}{dt} \\ $$$$\:\:{goal}\:::\:\:{I}=\frac{\mathrm{1}}{\mathrm{8}}{I}\:''\left(\mathrm{0}\right) \\ $$$$\:\:\:\:{but}\::\:\:{I}\left({a}\right)=\beta\left(\frac{\mathrm{1}}{\mathrm{2}}+{a},\frac{\mathrm{1}}{\mathrm{2}}−{a}\right)\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+{a}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{reflection}\:{formula}} {\overset{{euler}} {=}}\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{2}}+\pi{a}\right)}=\frac{\pi}{{cos}\left(\pi{a}\right)} \\ $$$$\:{I}\:'\left({a}\right)=\frac{\pi^{\mathrm{2}} {sin}\left(\pi{a}\right)}{{cos}^{\mathrm{2}} \left(\pi{a}\right)} \\ $$$$\:\:{I}\:''\left({a}\right)=\pi^{\mathrm{2}} \left(\frac{\pi{cos}^{\mathrm{3}} \left(\pi{a}\right)+\mathrm{2}\pi{sin}^{\mathrm{2}} \left(\pi{a}\right){cos}\left(\pi{a}\right)}{{cos}^{\mathrm{4}} \left(\pi{a}\right)}\right)\mid_{{a}=\mathrm{0}} \\ $$$$\:\:\:{I}\:''\left(\mathrm{0}\right)=\pi^{\mathrm{3}} \Rightarrow\:{I}=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}\:\:\checkmark\checkmark \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Nov/20
Great sir! i haven′t thought of this
$${Great}\:{sir}!\:{i}\:{haven}'{t}\:{thought}\:{of}\:{this} \\ $$
Commented by mnjuly1970 last updated on 23/Nov/20
thank you so much sir payan to me your solution is very very nice and unique...
$$\:\:\:{thank}\:{you}\:{so}\:{much}\:{sir}\:{payan} \\ $$$$\:\:{to}\:{me}\:{your}\:{solution}\:{is}\:{very}\:{very}\: \\ $$$${nice}\:{and}\:{unique}… \\ $$
Answered by Dwaipayan Shikari last updated on 23/Nov/20
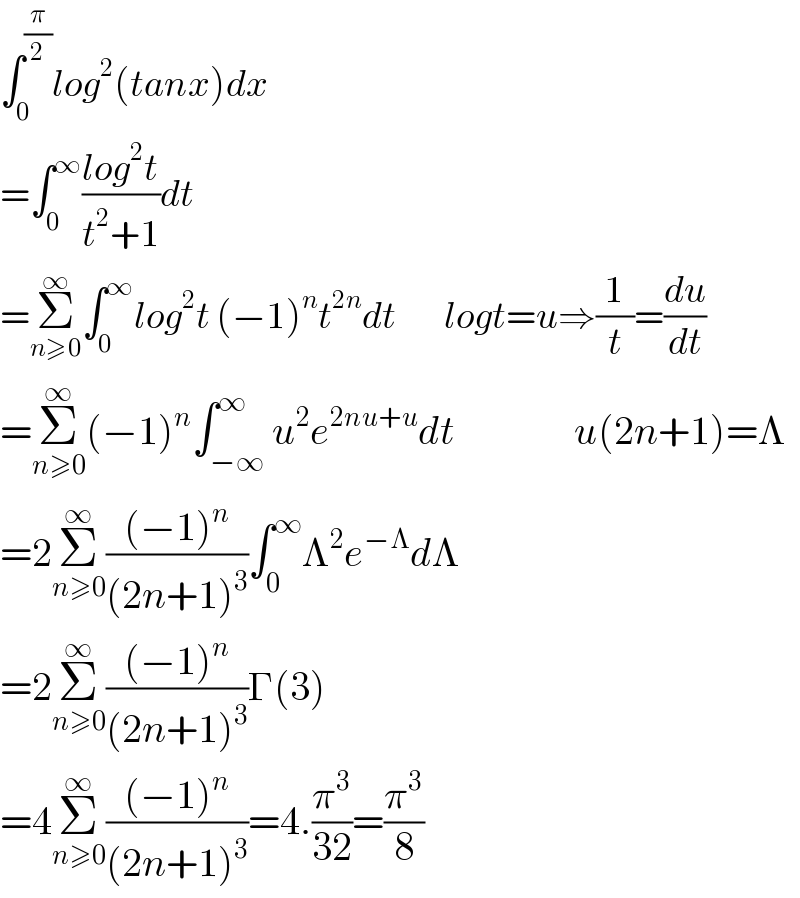
∫_0 ^(π/2) log^2 (tanx)dx =∫_0 ^∞ ((log^2 t)/(t^2 +1))dt =Σ_(n≥0) ^∞ ∫_0 ^∞ log^2 t (−1)^n t^(2n) dt logt=u⇒(1/t)=(du/dt) =Σ_(n≥0) ^∞ (−1)^n ∫_(−∞) ^∞ u^2 e^(2nu+u) dt u(2n+1)=Λ =2Σ_(n≥0) ^∞ (((−1)^n )/((2n+1)^3 ))∫_0 ^∞ Λ^2 e^(−Λ) dΛ =2Σ_(n≥0) ^∞ (((−1)^n )/((2n+1)^3 ))Γ(3) =4Σ_(n≥0) ^∞ (((−1)^n )/((2n+1)^3 ))=4.(π^3 /(32))=(π^3 /8)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}^{\mathrm{2}} \left({tanx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{log}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\: \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {log}^{\mathrm{2}} {t}\:\left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{2}{n}} {dt}\:\:\:\:\:\:\:\:{logt}={u}\Rightarrow\frac{\mathrm{1}}{{t}}=\frac{{du}}{{dt}} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{−\infty} ^{\infty} {u}^{\mathrm{2}} {e}^{\mathrm{2}{nu}+{u}} {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}\left(\mathrm{2}{n}+\mathrm{1}\right)=\Lambda \\ $$$$=\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} \Lambda^{\mathrm{2}} {e}^{−\Lambda} {d}\Lambda \\ $$$$=\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\Gamma\left(\mathrm{3}\right) \\ $$$$=\mathrm{4}\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{4}.\frac{\pi^{\mathrm{3}} }{\mathrm{32}}=\frac{\pi^{\mathrm{3}} }{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 23/Nov/20
very good ...
$${very}\:{good}\:… \\ $$
Commented by Lordose last updated on 23/Nov/20
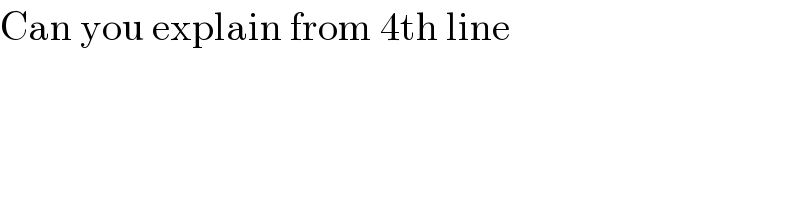
Can you explain from 4th line
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{from}\:\mathrm{4th}\:\mathrm{line} \\ $$
Commented by Dwaipayan Shikari last updated on 24/Nov/20
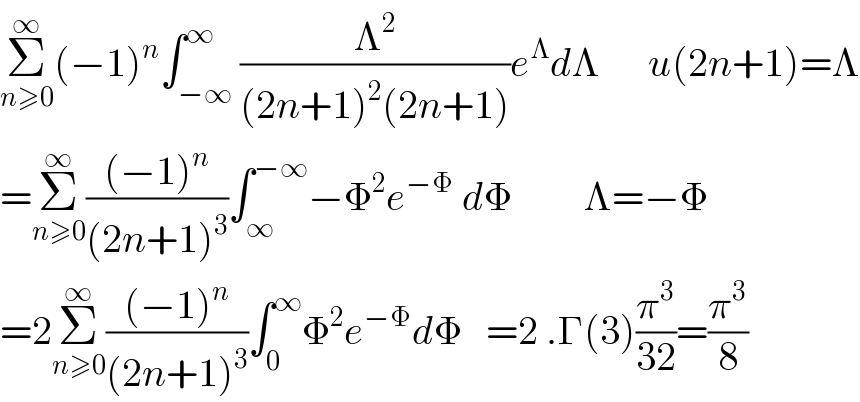
Σ_(n≥0) ^∞ (−1)^n ∫_(−∞) ^∞ (Λ^2 /((2n+1)^2 (2n+1)))e^Λ dΛ u(2n+1)=Λ =Σ_(n≥0) ^∞ (((−1)^n )/((2n+1)^3 ))∫_∞ ^(−∞) −Φ^2 e^(−Φ) dΦ Λ=−Φ =2Σ_(n≥0) ^∞ (((−1)^n )/((2n+1)^3 ))∫_0 ^∞ Φ^2 e^(−Φ) dΦ =2 .Γ(3)(π^3 /(32))=(π^3 /8)
$$\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{−\infty} ^{\infty} \frac{\Lambda^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}{e}^{\Lambda} {d}\Lambda\:\:\:\:\:\:{u}\left(\mathrm{2}{n}+\mathrm{1}\right)=\Lambda \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\int_{\infty} ^{−\infty} −\Phi^{\mathrm{2}} {e}^{−\Phi} \:{d}\Phi\:\:\:\:\:\:\:\:\:\Lambda=−\Phi \\ $$$$=\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} \Phi^{\mathrm{2}} {e}^{−\Phi} {d}\Phi\:\:\:=\mathrm{2}\:.\Gamma\left(\mathrm{3}\right)\frac{\pi^{\mathrm{3}} }{\mathrm{32}}=\frac{\pi^{\mathrm{3}} }{\mathrm{8}} \\ $$
Answered by mathmax by abdo last updated on 23/Nov/20
A =∫_0 ^(π/2) ln^2 (tanx)dx changementtanx=t give A =∫_0 ^∞ ((ln^2 (t))/(1+t^2 ))dt =∫_0 ^1 ((ln^2 (t))/(1+t^2 ))dt +∫_1 ^∞ ((ln^2 (t))/(1+t^2 ))dt (→t=(1/x)) =∫_0 ^1 ((ln^2 (t))/(1+t^2 ))dt −∫_0 ^1 ((ln^2 (x))/(1+(1/x^2 )))(−(dx/x^2 )) =2∫_0 ^1 ((ln^2 (x))/(1+x^2 ))dx =2∫_0 ^1 ln^2 (x)(Σ_(n=0) ^∞ (−1)^n x^(2n) )dx =2Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n) ln^2 (x)dx u_n =∫_0 ^(1 ) x^(2n) ln^2 (x)dx =[(x^(2n+1) /(2n+1))ln^2 (x)]_0 ^1 −∫_0 ^1 (x^(2n+1) /(2n+1))((2lnx)/x)dx =−(2/(2n+1))∫_0 ^1 x^(2n) ln(x)dx =−(2/(2n+1)){[(x^(2n+1) /(2n+1))lnx]_0 ^1 −∫_0 ^1 (x^(2n) /((2n+1)))dx} =(2/((2n+1)^3 )) ⇒ A =4 Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) rest to find tbe value of this serie by fourier....
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{tanx}\right)\mathrm{dx}\:\mathrm{changementtanx}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\left(\rightarrow\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\left(−\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }\right)\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx}\:=\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}\:} \mathrm{x}^{\mathrm{2n}} \:\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\frac{\mathrm{2lnx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=−\frac{\mathrm{2}}{\mathrm{2n}+\mathrm{1}}\left\{\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}+\mathrm{1}\right)}\mathrm{dx}\right\} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\:\mathrm{A}\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{tbe}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this} \\ $$$$\mathrm{serie}\:\mathrm{by}\:\mathrm{fourier}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *