Question Number 167164 by mnjuly1970 last updated on 08/Mar/22
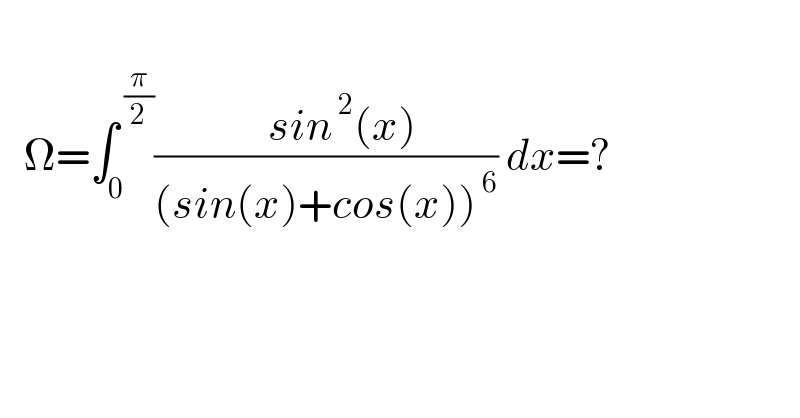
$$ \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\:\:\:\:{sin}^{\:\mathrm{2}} \left({x}\right)}{\left({sin}\left({x}\right)+{cos}\left({x}\right)\right)^{\:\mathrm{6}} }\:{dx}=? \\ $$
Answered by MJS_new last updated on 08/Mar/22
![∫((sin^2 x)/((sin x +cos x)^6 ))dx=∫((tan^2 x (1+tan^2 x)^2 )/((1+tan x)^6 ))dx [t=1+tan x → dx=cos^2 x dt] =∫(((t−1)^2 (t^2 −2t+2))/t^6 )dt= =∫((1/t^2 )−(4/t^3 )+(7/t^4 )−(6/t^5 )+(2/t^6 ))dt= =−(1/t)+(2/t^2 )−(7/(3t^3 ))+(3/(2t^4 ))−(2/(5t^5 ))= ... =−((30tan^4 x +60tan^3 x +70tan^2 x +35tan x +7)/(30(1+tan x)^5 ))+C](https://www.tinkutara.com/question/Q167166.png)
$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\left(\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\right)^{\mathrm{6}} }{dx}=\int\frac{\mathrm{tan}^{\mathrm{2}} \:{x}\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{6}} }{dx} \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{1}+\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\int\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{2}\right)}{{t}^{\mathrm{6}} }{dt}= \\ $$$$=\int\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{4}}{{t}^{\mathrm{3}} }+\frac{\mathrm{7}}{{t}^{\mathrm{4}} }−\frac{\mathrm{6}}{{t}^{\mathrm{5}} }+\frac{\mathrm{2}}{{t}^{\mathrm{6}} }\right){dt}= \\ $$$$=−\frac{\mathrm{1}}{{t}}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} }−\frac{\mathrm{7}}{\mathrm{3}{t}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{2}{t}^{\mathrm{4}} }−\frac{\mathrm{2}}{\mathrm{5}{t}^{\mathrm{5}} }= \\ $$$$… \\ $$$$=−\frac{\mathrm{30tan}^{\mathrm{4}} \:{x}\:+\mathrm{60tan}^{\mathrm{3}} \:{x}\:+\mathrm{70tan}^{\mathrm{2}} \:{x}\:+\mathrm{35tan}\:{x}\:+\mathrm{7}}{\mathrm{30}\left(\mathrm{1}+\mathrm{tan}\:{x}\right)^{\mathrm{5}} }+{C} \\ $$
