Menu Close

0-pi-2-sin-2-x-sin-x-cos-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 83805 by M±th+et£s last updated on 06/Mar/20
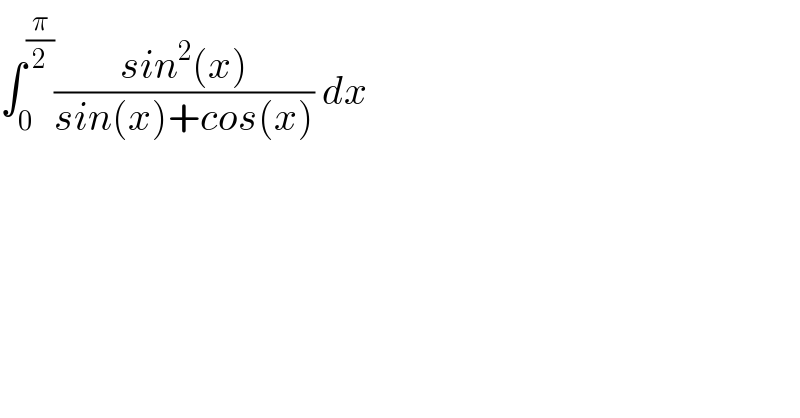
∫_0 ^(π/2) ((sin^2 (x))/(sin(x)+cos(x))) dx
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} \left({x}\right)}{{sin}\left({x}\right)+{cos}\left({x}\right)}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 06/Mar/20
A =∫_0 ^(π/2) ((sin^2 x)/(sinx +cosx))dx changement x=(π/2)−t give A =∫_0 ^(π/2) ((cos^2 t)/(cost +sint))dt =∫_0 ^(π/2) ((1−sin^2 t)/(cost +sint))dt =∫_0 ^(π/2) (dt/(cost +sint)) −A ⇒ 2A =∫_0 ^(π/2) (dt/(cost +sint)) =_(tan((t/2))=u) ∫_0 ^1 (1/(((1−u^2 )/(1+u^2 )) +((2u)/(1+u^2 ))))((2du)/(1+u^2 )) =2 ∫_0 ^1 (du/(1−u^2 +2u)) =−2 ∫_0 ^1 (du/(u^2 −2u−1)) =−2 ∫_0 ^1 (du/((u−1)^2 −2)) =−2 ∫_0 ^1 (du/((u−1−(√2))(u−1+(√2)))) =−(2/(2(√2)))∫_0 ^1 {(1/(u−1−(√2)))−(1/(u−1+(√2)))}du =−(1/( (√2)))[ln∣((u−1−(√2))/(u−1+(√2)))∣]_0 ^1 =−(1/( (√2))){−ln∣((−1−(√2))/(−1+(√2)))∣} =(1/( (√2)))ln((((√2) +1)/( (√2)−1))) ⇒A =(1/(2(√2)))ln((((√2) +1)/( (√2)−1)))
$${A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}^{\mathrm{2}} {x}}{{sinx}\:+{cosx}}{dx}\:{changement}\:{x}=\frac{\pi}{\mathrm{2}}−{t}\:{give} \\ $$$${A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cos}^{\mathrm{2}} {t}}{{cost}\:+{sint}}{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{sin}^{\mathrm{2}} {t}}{{cost}\:+{sint}}{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dt}}{{cost}\:+{sint}}\:−{A}\:\Rightarrow \\ $$$$\mathrm{2}{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dt}}{{cost}\:+{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} \:+\mathrm{2}{u}}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{du}}{\left({u}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({u}−\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{{u}−\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\right\}{du}\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[{ln}\mid\frac{{u}−\mathrm{1}−\sqrt{\mathrm{2}}}{{u}−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{−{ln}\mid\frac{−\mathrm{1}−\sqrt{\mathrm{2}}}{−\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right\}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)\:\Rightarrow{A}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$
Answered by MJS last updated on 06/Mar/20
∫((sin^2 x)/(sin x +cos x))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−8∫(t^2 /((t^2 +1)^2 (t^2 −2t−1)))dt= =2∫((t^2 +2t−1)/((t^2 +1)^2 ))dt−((√2)/4)∫(dt/(t−1−(√2)))+((√2)/4)∫(dt/(t−1+(√2)))= =−((t+1)/(t^2 +1))+((√2)/4)ln ((t−1+(√2))/(t−1−(√2))) =... =−((cos x +sin x)/2)+((√2)/4)ln ∣tan ((x/2)+(π/8))∣ +C ⇒ answer is ((√2)/8)ln (17+12(√2))
$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{8}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt}= \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{dt}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{dt}}{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}= \\ $$$$=−\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\frac{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\:=… \\ $$$$=−\frac{\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\mid\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\mid\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\left(\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}\right) \\ $$
Commented by Kamel Kamel last updated on 06/Mar/20
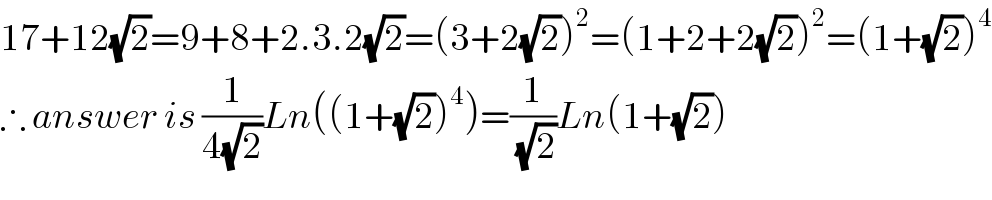
17+12(√2)=9+8+2.3.2(√2)=(3+2(√2))^2 =(1+2+2(√2))^2 =(1+(√2))^4 ∴ answer is (1/(4(√2)))Ln((1+(√2))^4 )=(1/( (√2)))Ln(1+(√2))
$$\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}=\mathrm{9}+\mathrm{8}+\mathrm{2}.\mathrm{3}.\mathrm{2}\sqrt{\mathrm{2}}=\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \\ $$$$\therefore\:{answer}\:{is}\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{Ln}\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{Ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Answered by Kamel Kamel last updated on 06/Mar/20
Put: Ω=∫_0 ^(π/2) ((sin^2 (x))/(sin(x)+cos(x)))dx=^(t=(π/2)−x) ∫_0 ^(π/2) ((cos^2 (t))/(cos(t)+sin(t)))dt ∴ Ω=(1/2)∫_0 ^(π/2) (dx/(sin(x)+cos(x)))=(1/(2(√2)))∫_0 ^(π/2) (dx/(sin((π/4)+x))) ∫(dx/(sin(x)))=^(t=tg((x/2))) ∫(dt/t)=Ln∣tg((x/2))∣+c ∴ Ω=(1/(2(√2)))(Ln∣tg((π/8)+(π/4))∣−Ln∣tg((π/8))∣) =(1/(2(√2)))(Ln∣tg((π/2)−(π/8))∣−Ln∣tg((π/8))∣ cos(2(π/8))=2cos^2 ((π/8))−1⇒cos^2 ((π/8))=((1+(√2))/(2(√2))) ∴ tg((π/8))=(√(((2(√2))/(1+(√2)))−1))=(√(((√2)−1)/( (√2)+1)))=(√2)−1 ∴ Ω=−(1/( (√2)))Ln(tg((π/8)))=−(1/( (√2)))Ln((√2)−1)=(1/( (√2)))Ln(1+(√2)) KAMEL BENAICHA
$${Put}:\:\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} \left({x}\right)}{{sin}\left({x}\right)+{cos}\left({x}\right)}{dx}\overset{{t}=\frac{\pi}{\mathrm{2}}−{x}} {=}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} \left({t}\right)}{{cos}\left({t}\right)+{sin}\left({t}\right)}{dt} \\ $$$$\therefore\:\Omega=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{sin}\left({x}\right)+{cos}\left({x}\right)}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)} \\ $$$$\int\frac{{dx}}{{sin}\left({x}\right)}\overset{{t}={tg}\left(\frac{{x}}{\mathrm{2}}\right)} {=}\:\:\:\:\int\frac{{dt}}{{t}}={Ln}\mid{tg}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{c} \\ $$$$\therefore\:\Omega=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left({Ln}\mid{tg}\left(\frac{\pi}{\mathrm{8}}+\frac{\pi}{\mathrm{4}}\right)\mid−{Ln}\mid{tg}\left(\frac{\pi}{\mathrm{8}}\right)\mid\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left({Ln}\mid{tg}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right)\mid−{Ln}\mid{tg}\left(\frac{\pi}{\mathrm{8}}\right)\mid\right. \\ $$$${cos}\left(\mathrm{2}\frac{\pi}{\mathrm{8}}\right)=\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)−\mathrm{1}\Rightarrow{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\therefore\:{tg}\left(\frac{\pi}{\mathrm{8}}\right)=\sqrt{\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}−\mathrm{1}}=\sqrt{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\therefore\:\Omega=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{Ln}\left({tg}\left(\frac{\pi}{\mathrm{8}}\right)\right)=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{Ln}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{Ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{KAMEL}}\:\boldsymbol{{BENAICHA}} \\ $$
Answered by TANMAY PANACEA last updated on 06/Mar/20
I=∫_0 ^(π/2) ((sin^2 x)/(sinx+cosx))dx =∫_0 ^(π/2) ((sin^2 ((π/2)−x))/(sin((π/2)−x)+cos((π/2)−x)))dx=∫_0 ^(π/2) ((cos^2 x)/(cosx+sinx))dx 2I=∫_0 ^(π/2) (dx/( (√2) (sin(π/4)cosx+cos(π/4)sinx))) I=(1/(2(√2)))∫_0 ^(π/2) cosec(x+(π/4))dx =(1/(2(√2)))∣lntan((x/2)+(π/8))∣_0 ^(π/2) =(1/(2(√2)))(lntan((π/4)+(π/8))−lntan((π/8))) tan(π/8)=a (1/(2(√2)))(ln(((1+a)/(1−a)))−lna)=(1/(2(√2)))ln(((1+a)/(a−a^2 )))
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} {x}}{{sinx}+{cosx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {x}}{{cosx}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\:\sqrt{\mathrm{2}}\:\left({sin}\frac{\pi}{\mathrm{4}}{cosx}+{cos}\frac{\pi}{\mathrm{4}}{sinx}\right)} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosec}\left({x}+\frac{\pi}{\mathrm{4}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{lntan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left({lntan}\left(\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{8}}\right)−{lntan}\left(\frac{\pi}{\mathrm{8}}\right)\right) \\ $$$${tan}\frac{\pi}{\mathrm{8}}={a} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left({ln}\left(\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\right)−{lna}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+{a}}{{a}−{a}^{\mathrm{2}} }\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *