Question Number 97109 by student work last updated on 06/Jun/20
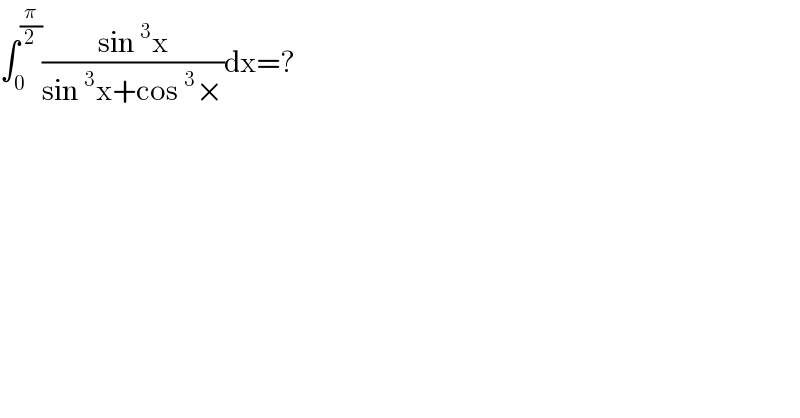
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} ×}\mathrm{dx}=? \\ $$
Answered by Sourav mridha last updated on 06/Jun/20
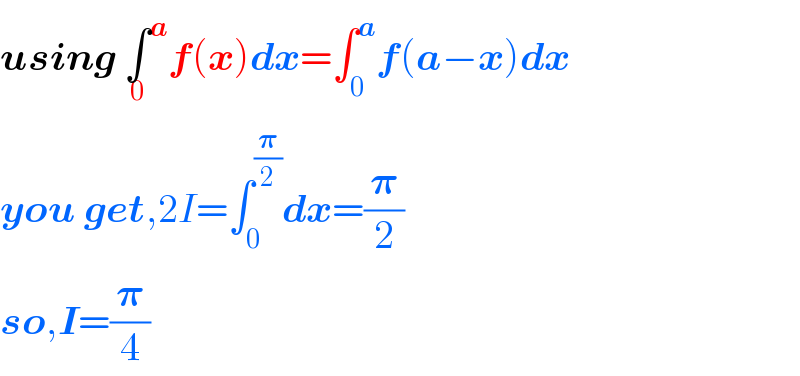
$$\boldsymbol{{using}}\:\underset{\mathrm{0}} {\int}^{\boldsymbol{{a}}} \boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}=\int_{\mathrm{0}} ^{\boldsymbol{{a}}} \boldsymbol{{f}}\left(\boldsymbol{{a}}−\boldsymbol{{x}}\right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{you}}\:\boldsymbol{{get}},\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{dx}}=\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}},\boldsymbol{{I}}=\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$
Commented by student work last updated on 06/Jun/20

$$\mathrm{how}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}? \\ $$
Answered by Sourav mridha last updated on 06/Jun/20
![I=∫_0 ^(π/2) ((sin^3 (x))/(sin^3 (x)+cos^3 (x)))dx..(i) also I=∫_0 ^(π/2) ((sin^3 ((π/2)−x))/(sin^3 ((π/2)−x)+cos^3 ((π/2)−x)))dx =∫_0 ^(π/2) ((cos^3 (x))/(cos^3 (x)+sin^3 (x)))dx..(ii) now (i)+(ii),2I=∫_0 ^(π/2) dx=[(π/2)−0] so I=(π/4)](https://www.tinkutara.com/question/Q97140.png)
$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{x}\right)}{\mathrm{sin}^{\mathrm{3}} \left(\mathrm{x}\right)+\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)}\mathrm{dx}..\left(\mathrm{i}\right) \\ $$$$\mathrm{also}\:\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}{\mathrm{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)+\mathrm{cos}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)}{\mathrm{cos}^{\mathrm{3}} \left(\mathrm{x}\right)+\mathrm{sin}^{\mathrm{3}} \left(\mathrm{x}\right)}\mathrm{dx}..\left(\mathrm{ii}\right) \\ $$$$\mathrm{now}\:\left(\mathrm{i}\right)+\left(\mathrm{ii}\right),\mathrm{2}\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{dx}=\left[\frac{\pi}{\mathrm{2}}−\mathrm{0}\right] \\ $$$$\:\:\:\:\mathrm{so}\:\boldsymbol{{I}}=\frac{\pi}{\mathrm{4}}\:\:\:\:\:\: \\ $$
