Menu Close

0-pi-2-sin-n-x-dx-In-closed-form-n-N-

Tinku Tara 0 Comments
Pin




Question Number 121983 by Dwaipayan Shikari last updated on 13/Nov/20
∫_0 ^(π/2) sin^n x dx (In closed form) (n∈N)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{n}} {x}\:{dx}\:\left({In}\:{closed}\:{form}\right)\:\:\left({n}\in\mathbb{N}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 13/Nov/20
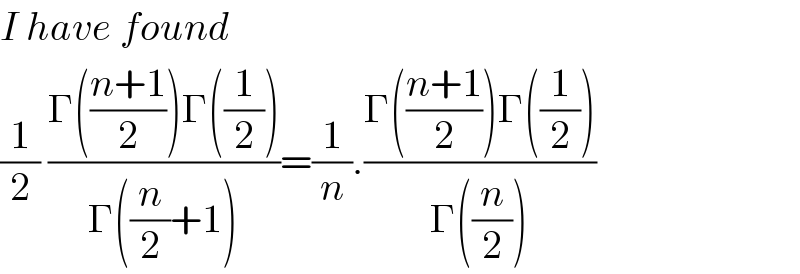
I have found (1/2) ((Γ(((n+1)/2))Γ((1/2)))/(Γ((n/2)+1)))=(1/n).((Γ(((n+1)/2))Γ((1/2)))/(Γ((n/2))))
$${I}\:{have}\:{found} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{n}}{\mathrm{2}}+\mathrm{1}\right)}=\frac{\mathrm{1}}{{n}}.\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{n}}{\mathrm{2}}\right)} \\ $$
Commented by mnjuly1970 last updated on 13/Nov/20
perfect mr dwaipayan..
$${perfect}\:\:{mr}\:\:{dwaipayan}.. \\ $$
Answered by mnjuly1970 last updated on 13/Nov/20
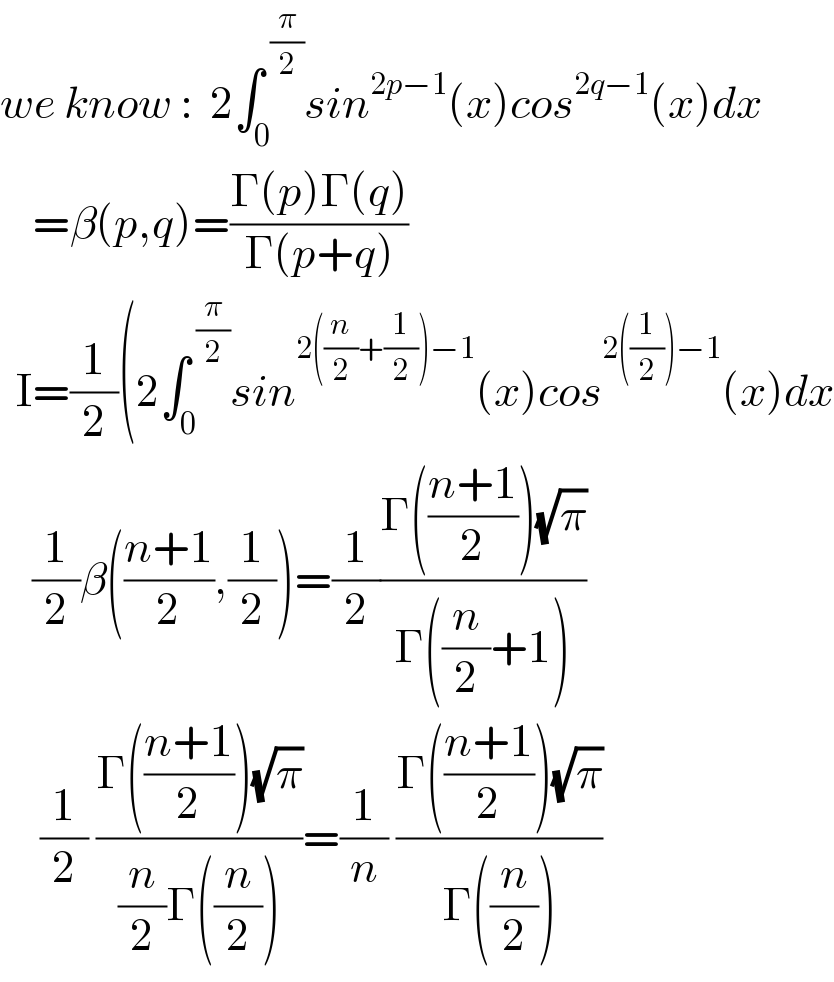
we know : 2∫_0 ^( (π/2)) sin^(2p−1) (x)cos^(2q−1) (x)dx =β(p,q)=((Γ(p)Γ(q))/(Γ(p+q))) I=(1/2)(2∫_0 ^( (π/2)) sin^(2((n/2)+(1/2))−1) (x)cos^(2((1/2))−1) (x)dx (1/2)β(((n+1)/2),(1/2))=(1/2)((Γ(((n+1)/2))(√π))/(Γ((n/2)+1))) (1/2) ((Γ(((n+1)/2))(√π))/((n/2)Γ((n/2))))=(1/n) ((Γ(((n+1)/2))(√π))/(Γ((n/2))))
$${we}\:{know}\::\:\:\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{p}−\mathrm{1}} \left({x}\right){cos}^{\mathrm{2}{q}−\mathrm{1}} \left({x}\right){dx} \\ $$$$\:\:\:\:=\beta\left({p},{q}\right)=\frac{\Gamma\left({p}\right)\Gamma\left({q}\right)}{\Gamma\left({p}+{q}\right)} \\ $$$$\:\:\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}\left(\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \left({x}\right){cos}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \left({x}\right){dx}\right. \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{{n}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\Gamma\left(\frac{{n}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\frac{{n}}{\mathrm{2}}\Gamma\left(\frac{{n}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{{n}}\:\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\Gamma\left(\frac{{n}}{\mathrm{2}}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Nov/20
Thanking you for confirmation sir!
$${Thanking}\:{you}\:{for}\:{confirmation}\:{sir}! \\ $$
Commented by mnjuly1970 last updated on 13/Nov/20
you are welcom .mr Dwaipayan grateful for your nice questions..
$$\:{you}\:{are}\:{welcom}\:.{mr}\:{Dwaipayan} \\ $$$${grateful}\:{for}\:{your}\:{nice}\:{questions}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *