Question Number 183109 by cortano1 last updated on 20/Dec/22
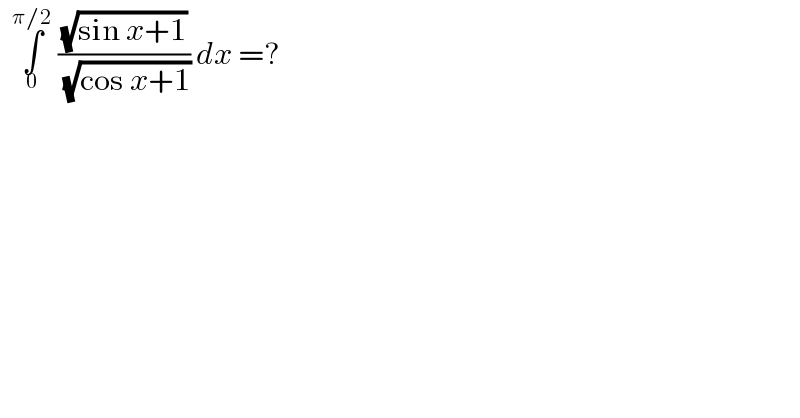
$$\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\sqrt{\mathrm{sin}\:{x}+\mathrm{1}}}{\:\sqrt{\mathrm{cos}\:{x}+\mathrm{1}}}\:{dx}\:=?\: \\ $$
Answered by universe last updated on 20/Dec/22
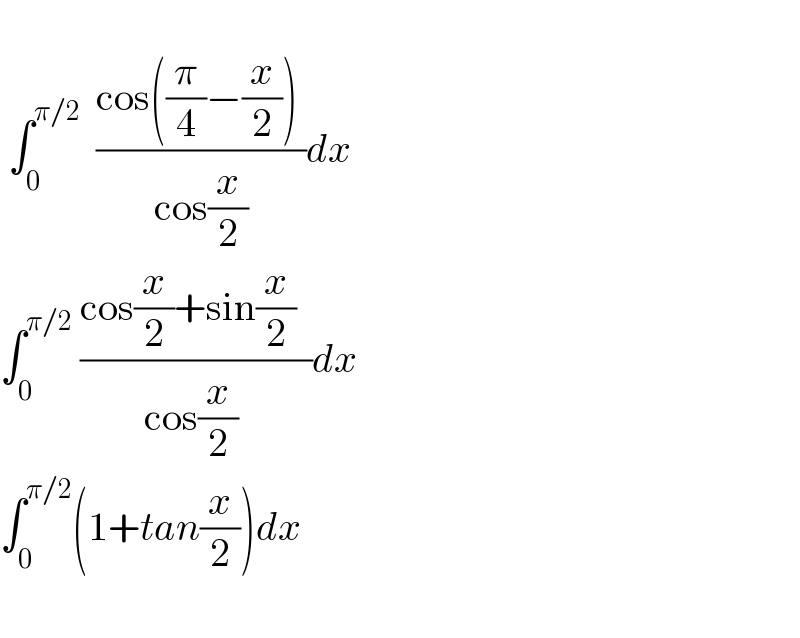
$$ \\ $$$$\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\:\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\:}{\:\mathrm{cos}\frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}\:\:}{\mathrm{cos}\frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{1}+{tan}\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\:\: \\ $$
Commented by MJS_new last updated on 21/Dec/22

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}{dx}\approx\mathrm{1}.\mathrm{60} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\left(\mathrm{1}+\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right){dx}\approx\mathrm{2}.\mathrm{26} \\ $$
Answered by MJS_new last updated on 21/Dec/22
![∫_0 ^(π/2) ((√(1+sin x))/( (√(1+cos x))))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =(√2)∫_0 ^1 ((t+1)/(t^2 +1))dt= =(√2)[(1/2)ln (t^2 +1) +arctan t]_0 ^1 = =((π(√2))/4)+((√2)/2)ln 2](https://www.tinkutara.com/question/Q183147.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=\sqrt{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\mathrm{arctan}\:{t}\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$
Commented by cortano1 last updated on 21/Dec/22

$${yess}…. \\ $$
