Question Number 189266 by cortano12 last updated on 14/Mar/23
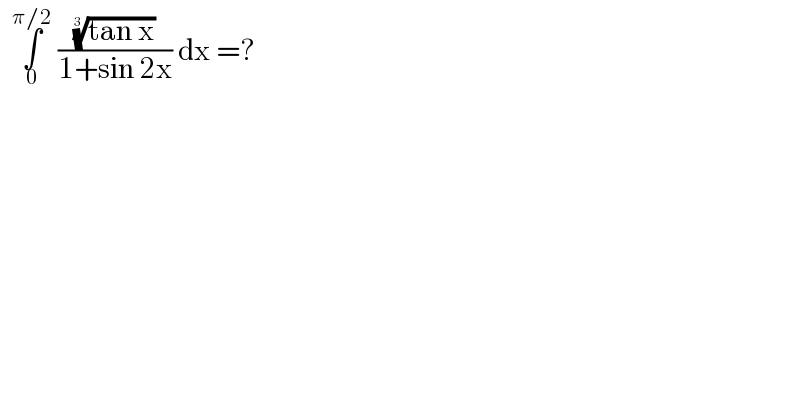
$$\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:\mathrm{x}}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}\:\mathrm{dx}\:=? \\ $$
Answered by MJS_new last updated on 14/Mar/23
![∫(((tan x))^(1/3) /(1+sin 2x))dx= [t=((tan x))^(1/3) → dx=3cos^2 x ((tan^2 x))^(1/3) dt] =3∫(t^3 /((t^3 +1)^2 ))dt= [Ostrogradski′s Method] =−(t/(t^3 +1))+∫(dt/(t^3 +1))= [decompose etc.] =−(t/(t^3 +1))+((√3)/3)arctan (((√3)(2t−1))/3) +(1/6)ln (((t+1)^2 )/(t^2 −t+1)) borders for t are 0≤t<∞ ⇒ answer is ((2(√3)π)/9)](https://www.tinkutara.com/question/Q189301.png)
$$\int\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{3cos}^{\mathrm{2}} \:{x}\:\sqrt[{\mathrm{3}}]{\mathrm{tan}^{\mathrm{2}} \:{x}}\:{dt}\right] \\ $$$$=\mathrm{3}\int\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{{t}}{{t}^{\mathrm{3}} +\mathrm{1}}+\int\frac{{dt}}{{t}^{\mathrm{3}} +\mathrm{1}}= \\ $$$$\:\:\:\:\:\left[\mathrm{decompose}\:\mathrm{etc}.\right] \\ $$$$=−\frac{{t}}{{t}^{\mathrm{3}} +\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} −{t}+\mathrm{1}} \\ $$$$\mathrm{borders}\:\mathrm{for}\:{t}\:\mathrm{are}\:\mathrm{0}\leqslant{t}<\infty\:\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi}{\mathrm{9}} \\ $$
