Question Number 185880 by cortano1 last updated on 29/Jan/23
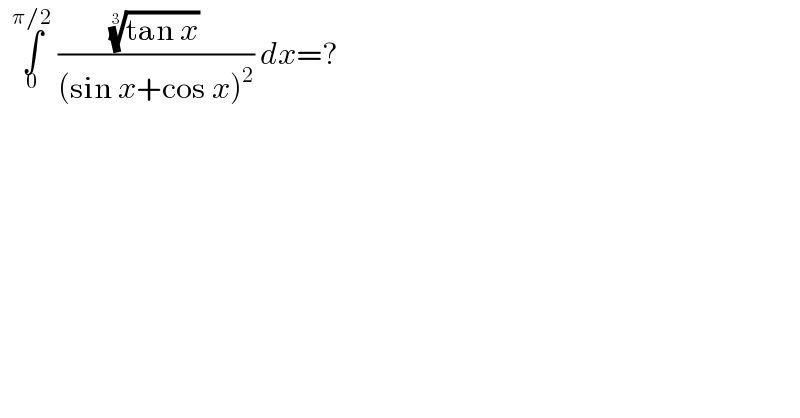
$$\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}}{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}=? \\ $$
Commented by MJS_new last updated on 29/Jan/23
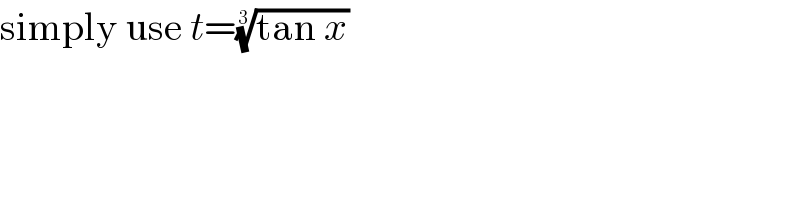
$$\mathrm{simply}\:\mathrm{use}\:{t}=\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}} \\ $$
Commented by cortano1 last updated on 29/Jan/23

Answered by cortano1 last updated on 29/Jan/23
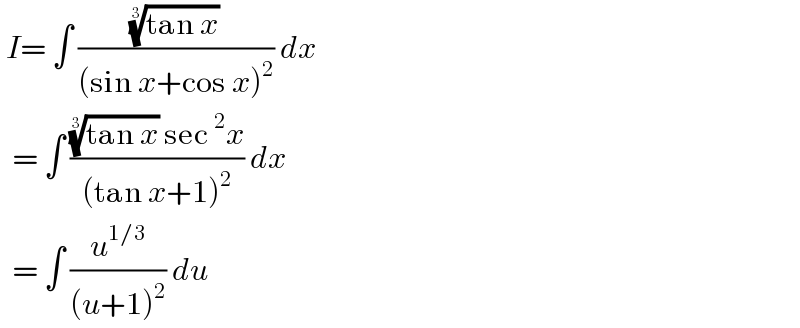
$$\:{I}=\:\int\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}}{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\:\:=\:\int\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}\:\mathrm{sec}\:^{\mathrm{2}} {x}}{\left(\mathrm{tan}\:{x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\:\:=\:\int\:\frac{{u}^{\mathrm{1}/\mathrm{3}} }{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:{du}\: \\ $$
Commented by cortano1 last updated on 29/Jan/23

$${it}'{s}\:{correct}? \\ $$
Answered by MJS_new last updated on 29/Jan/23
![∫_0 ^(π/2) (((tan x))^(1/3) /((sin x +cos x)))dx= [t=((tan x))^(1/3) → dx=3cos^2 x ((tan^2 x))^(1/3) dx] =3∫_0 ^∞ (t^3 /((t^3 +1)^2 ))dt= [Ostrogradski′s Method] =[−(t/(t^3 +1))]_0 ^∞ +∫_0 ^∞ (dt/(t^3 +1))= =0+[(1/6)ln (((t+1)^2 )/(t^2 −t+1)) +((√3)/3)arctan (((√3)(2t−1))/3)]_0 ^∞ = =((2(√3))/9)π](https://www.tinkutara.com/question/Q185914.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}}{\left(\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{3}}]{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{3cos}^{\mathrm{2}} \:{x}\:\sqrt[{\mathrm{3}}]{\mathrm{tan}^{\mathrm{2}} \:{x}}{dx}\right] \\ $$$$=\mathrm{3}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\left[−\frac{{t}}{{t}^{\mathrm{3}} +\mathrm{1}}\right]_{\mathrm{0}} ^{\infty} +\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{3}} +\mathrm{1}}= \\ $$$$=\mathrm{0}+\left[\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$
Commented by cortano1 last updated on 30/Jan/23

$${thank}\:{you} \\ $$
