Question Number 54971 by peter frank last updated on 15/Feb/19
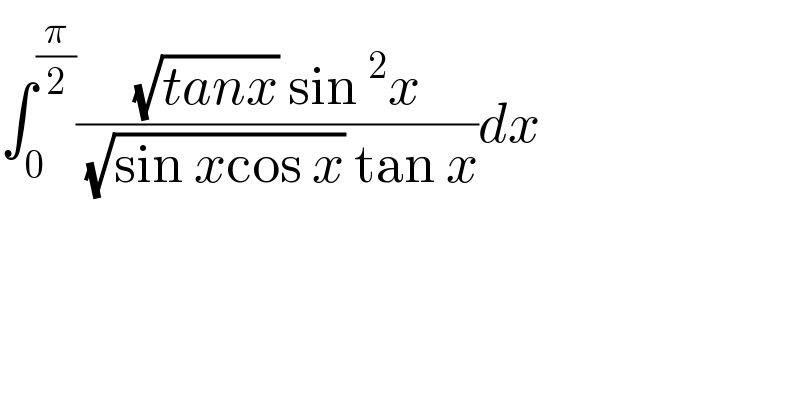
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{{tanx}}\:\mathrm{sin}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{sin}\:{x}\mathrm{cos}\:{x}}\:\mathrm{tan}\:{x}}{dx} \\ $$
Answered by kaivan.ahmadi last updated on 15/Feb/19
![∫_0 ^(π/2) (((√((sinx)/(cosx)))sin^2 x)/( (√(sinxcosx))((sinx)/(cosx))))dx= ∫_0 ^(π/2) sinxdx=−cosx]_0 ^(π/2) =1](https://www.tinkutara.com/question/Q54979.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{\frac{{sinx}}{{cosx}}}{sin}^{\mathrm{2}} {x}}{\:\sqrt{{sinxcosx}}\frac{{sinx}}{{cosx}}}{dx}= \\ $$$$\left.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sinxdx}=−{cosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Feb/19
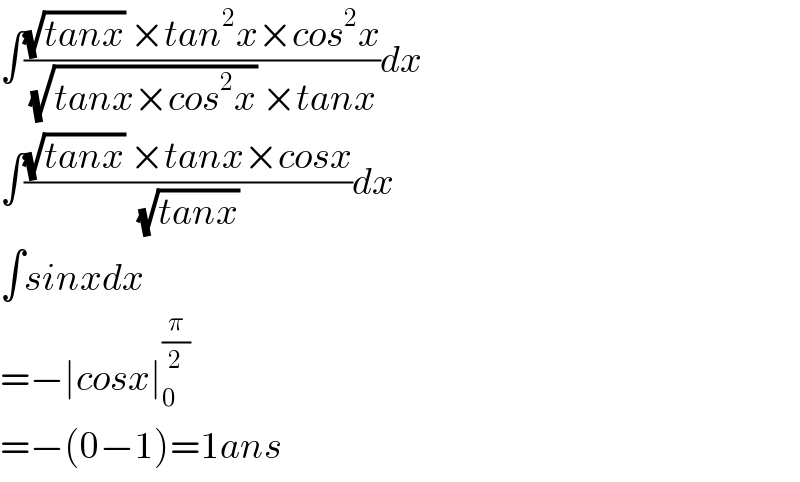
$$\int\frac{\sqrt{{tanx}}\:×{tan}^{\mathrm{2}} {x}×{cos}^{\mathrm{2}} {x}}{\:\sqrt{{tanx}×{cos}^{\mathrm{2}} {x}}\:×{tanx}}{dx} \\ $$$$\int\frac{\sqrt{{tanx}}\:×{tanx}×{cosx}}{\:\sqrt{{tanx}}\:}{dx} \\ $$$$\int{sinxdx} \\ $$$$=−\mid{cosx}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \: \\ $$$$=−\left(\mathrm{0}−\mathrm{1}\right)=\mathrm{1}{ans} \\ $$
