Question Number 130958 by bramlexs22 last updated on 31/Jan/21
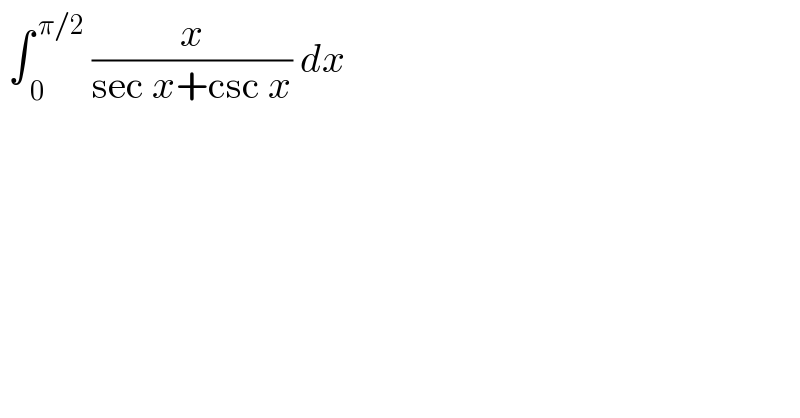
$$\:\int_{\:\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{{x}}{\mathrm{sec}\:{x}+\mathrm{csc}\:{x}}\:{dx} \\ $$
Commented by benjo_mathlover last updated on 31/Jan/21
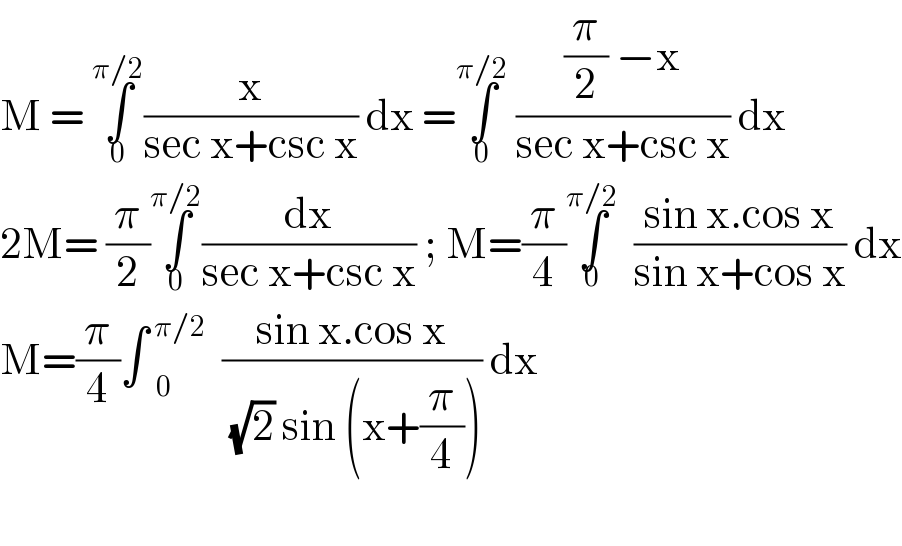
$$\mathrm{M}\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{x}}{\mathrm{sec}\:\mathrm{x}+\mathrm{csc}\:\mathrm{x}}\:\mathrm{dx}\:=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\frac{\pi}{\mathrm{2}}\:−\mathrm{x}}{\mathrm{sec}\:\mathrm{x}+\mathrm{csc}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{2M}=\:\frac{\pi}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{dx}}{\mathrm{sec}\:\mathrm{x}+\mathrm{csc}\:\mathrm{x}}\:;\:\mathrm{M}=\frac{\pi}{\mathrm{4}}\overset{\pi/\mathrm{2}} {\int}_{\mathrm{0}} \frac{\mathrm{sin}\:\mathrm{x}.\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{M}=\frac{\pi}{\mathrm{4}}\int\overset{\:\pi/\mathrm{2}} {\:}_{\mathrm{0}} \frac{\mathrm{sin}\:\mathrm{x}.\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}\:\mathrm{dx} \\ $$$$ \\ $$
Commented by benjo_mathlover last updated on 31/Jan/21
![M=(π/(4(√2))) ∫_(π/4) ^(3π/4) (((1/( (√2)))(sin t−cos t).(1/( (√2)))(cos t+sin t))/(sin t)) dt M= (π/(8(√2) ))∫_(π/4) ^(3π/4) ((2sin^2 t−1 )/(sin t)) dt = (π/(8(√2)))(−2cos t+ln ∣csc t + cot t ∣ )_(π/4) ^(3π/4) M= (π/( 4(√2))) [ (√2) +ln ((√2)−1) ]](https://www.tinkutara.com/question/Q130997.png)
$$\mathrm{M}=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{sin}\:\mathrm{t}−\mathrm{cos}\:\mathrm{t}\right).\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{cos}\:\mathrm{t}+\mathrm{sin}\:\mathrm{t}\right)}{\mathrm{sin}\:\mathrm{t}}\:\mathrm{dt} \\ $$$$\mathrm{M}=\:\frac{\pi}{\mathrm{8}\sqrt{\mathrm{2}}\:}\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\frac{\mathrm{2sin}^{\mathrm{2}} \:\mathrm{t}−\mathrm{1}\:}{\mathrm{sin}\:\mathrm{t}}\:\mathrm{dt}\:=\:\frac{\pi}{\mathrm{8}\sqrt{\mathrm{2}}}\left(−\mathrm{2cos}\:\mathrm{t}+\mathrm{ln}\:\mid\mathrm{csc}\:\mathrm{t}\:+\:\mathrm{cot}\:\mathrm{t}\:\mid\:\right)_{\pi/\mathrm{4}} ^{\mathrm{3}\pi/\mathrm{4}} \\ $$$$\mathrm{M}=\:\frac{\pi}{\:\mathrm{4}\sqrt{\mathrm{2}}}\:\left[\:\sqrt{\mathrm{2}}\:+\mathrm{ln}\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\:\right]\: \\ $$
