Menu Close

0-pi-2-x-sin-x-cos-x-cos-4-x-sin-4-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 161212 by cortano last updated on 14/Dec/21
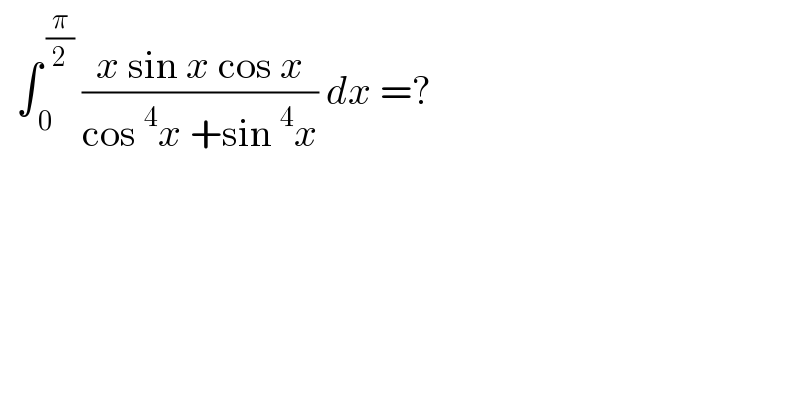
∫_( 0) ^( (π/2)) ((x sin x cos x)/(cos^4 x +sin^4 x)) dx =?
$$\:\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{cos}\:^{\mathrm{4}} {x}\:+\mathrm{sin}\:^{\mathrm{4}} {x}}\:{dx}\:=? \\ $$
Commented by puissant last updated on 15/Dec/21
Commented by Tawa11 last updated on 15/Dec/21
Nice sirs
$$\mathrm{Nice}\:\mathrm{sirs} \\ $$
Answered by chhaythean last updated on 14/Dec/21
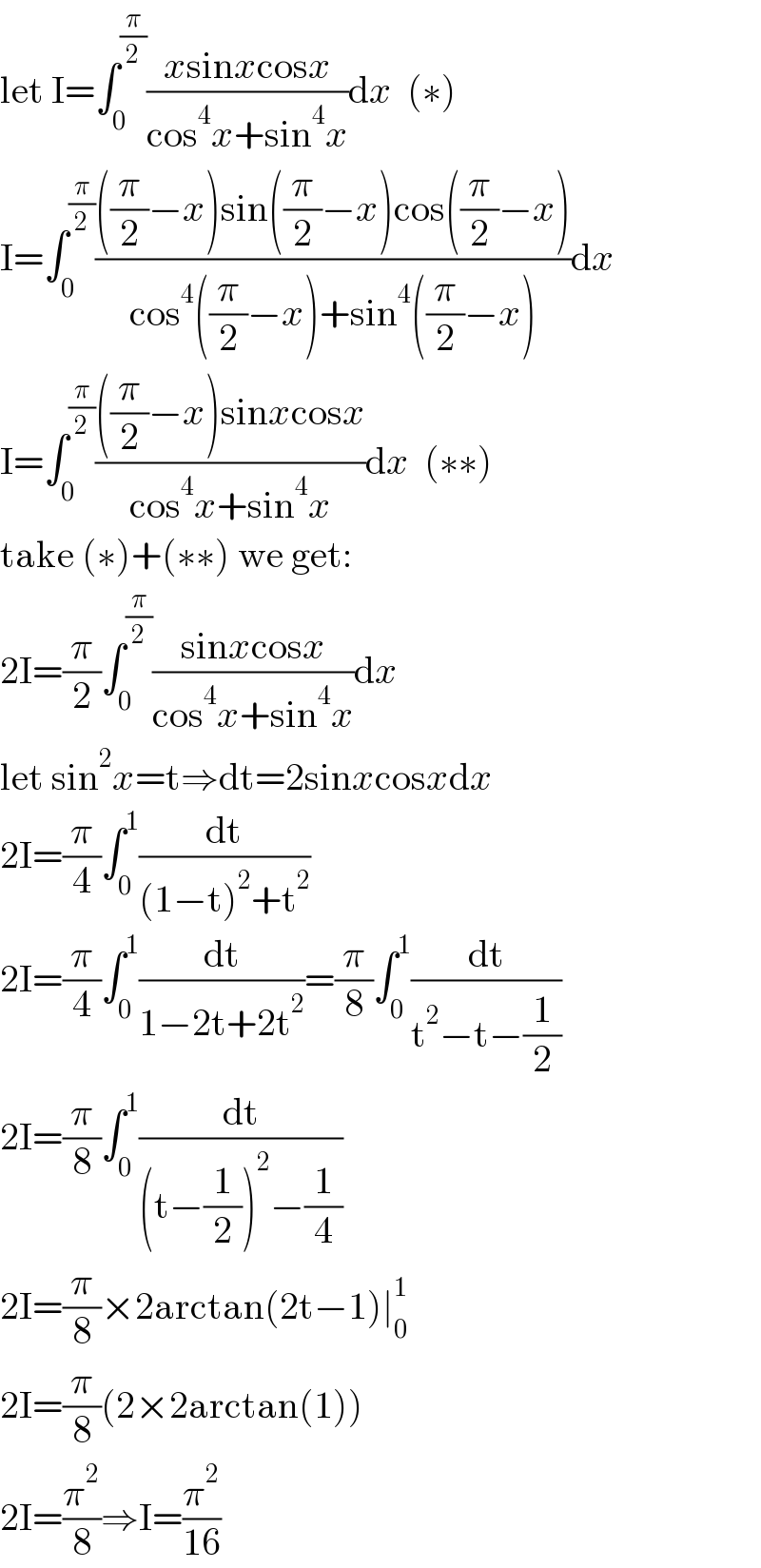
let I=∫_0 ^(π/2) ((xsinxcosx)/(cos^4 x+sin^4 x))dx (∗) I=∫_0 ^(π/2) ((((π/2)−x)sin((π/2)−x)cos((π/2)−x))/(cos^4 ((π/2)−x)+sin^4 ((π/2)−x)))dx I=∫_0 ^(π/2) ((((π/2)−x)sinxcosx)/(cos^4 x+sin^4 x))dx (∗∗) take (∗)+(∗∗) we get: 2I=(π/2)∫_0 ^(π/2) ((sinxcosx)/(cos^4 x+sin^4 x))dx let sin^2 x=t⇒dt=2sinxcosxdx 2I=(π/4)∫_0 ^1 (dt/((1−t)^2 +t^2 )) 2I=(π/4)∫_0 ^1 (dt/(1−2t+2t^2 ))=(π/8)∫_0 ^1 (dt/(t^2 −t−(1/2))) 2I=(π/8)∫_0 ^1 (dt/((t−(1/2))^2 −(1/4))) 2I=(π/8)×2arctan(2t−1)∣_0 ^1 2I=(π/8)(2×2arctan(1)) 2I=(π^2 /8)⇒I=(π^2 /(16))
$$\mathrm{let}\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}\mathrm{sin}{x}\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{4}} {x}}\mathrm{d}{x}\:\:\left(\ast\right) \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\frac{\pi}{\mathrm{2}}−{x}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)+\mathrm{sin}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}\mathrm{d}{x} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\frac{\pi}{\mathrm{2}}−{x}\right)\mathrm{sin}{x}\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{4}} {x}}\mathrm{d}{x}\:\:\left(\ast\ast\right) \\ $$$$\mathrm{take}\:\left(\ast\right)+\left(\ast\ast\right)\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}{x}\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{4}} {x}}\mathrm{d}{x} \\ $$$$\mathrm{let}\:\mathrm{sin}^{\mathrm{2}} {x}=\mathrm{t}\Rightarrow\mathrm{dt}=\mathrm{2sin}{x}\mathrm{cos}{x}\mathrm{d}{x} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{1}−\mathrm{2t}+\mathrm{2t}^{\mathrm{2}} }=\frac{\pi}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{8}}×\mathrm{2arctan}\left(\mathrm{2t}−\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{2I}=\frac{\pi}{\mathrm{8}}\left(\mathrm{2}×\mathrm{2arctan}\left(\mathrm{1}\right)\right) \\ $$$$\mathrm{2I}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\Rightarrow\mathrm{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$
Commented by cortano last updated on 14/Dec/21
yes. thanks
$${yes}.\:{thanks} \\ $$
Answered by Ar Brandon last updated on 14/Dec/21
I=∫_0 ^(π/2) ((xsinxcosx)/(cos^4 x+sin^4 x))dx=(π/4)∫_0 ^(π/2) ((sinxcosx)/(cos^4 x+sin^4 x))dx =(π/4)∫_0 ^(π/2) ((tanx∙sec^2 x)/(1+tan^4 x))dx=(π/4)∫_0 ^∞ (t/(t^4 +1))dt =(π/8)∫_0 ^∞ (du/(u^2 +1))=(π/8)[tan^(−1) (u)]_0 ^∞ =(π^2 /(16))
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}\mathrm{sin}{x}\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{4}} {x}}{dx}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}{x}\mathrm{cos}{x}}{\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{4}} {x}}{dx} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{tan}{x}\centerdot\mathrm{sec}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{tan}^{\mathrm{4}} {x}}{dx}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{t}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{8}}\int_{\mathrm{0}} ^{\infty} \frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\pi}{\mathrm{8}}\left[\mathrm{tan}^{−\mathrm{1}} \left({u}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$
Commented by Ar Brandon last updated on 14/Dec/21
u=t^2 , t=tanx
$$\:\:\:\:\:{u}={t}^{\mathrm{2}} ,\:\:{t}=\mathrm{tan}{x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *