Question Number 80416 by jagoll last updated on 03/Feb/20
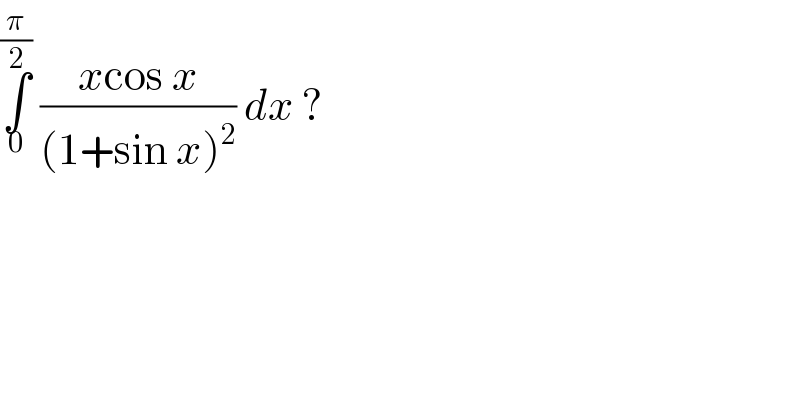
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{x}\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:{dx}\:? \\ $$
Answered by MJS last updated on 03/Feb/20
![∫((xcos x)/((1+sin x)^2 ))dx= by parts u=x → u′=1 v′=((cos x)/((1+sin x)^2 )) → v=−(1/(1+sin x)) =−(x/(1+sin x))+∫(dx/(1+sin x))= =−(x/(1+sin x))+tan x −(1/(cos x))+C ∫_0 ^(π/2) ((xcos x)/((1+sin x)^2 ))dx= [lim_(x→(π/2)) (tan x −(1/(cos x)))=0] =1−(π/4)](https://www.tinkutara.com/question/Q80418.png)
$$\int\frac{{x}\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\:\:\:\:\:{u}={x}\:\rightarrow\:{u}'=\mathrm{1} \\ $$$$\:\:\:\:\:{v}'=\frac{\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:\rightarrow\:{v}=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$$$=−\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}+\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}= \\ $$$$=−\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}+\mathrm{tan}\:{x}\:−\frac{\mathrm{1}}{\mathrm{cos}\:{x}}+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{x}\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left(\mathrm{tan}\:{x}\:−\frac{\mathrm{1}}{\mathrm{cos}\:{x}}\right)=\mathrm{0}\right] \\ $$$$=\mathrm{1}−\frac{\pi}{\mathrm{4}} \\ $$
Commented by jagoll last updated on 03/Feb/20
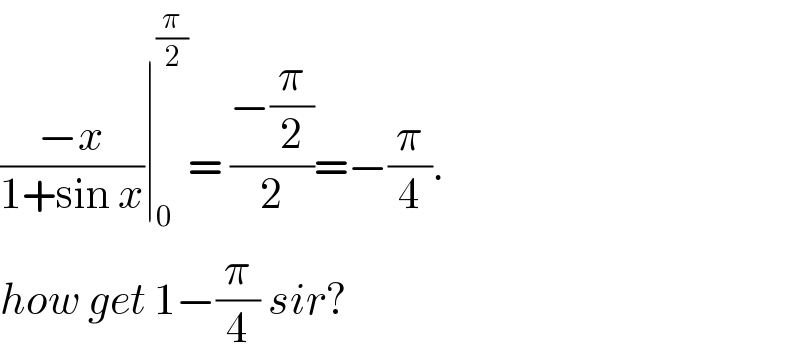
$$\frac{−{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\frac{−\frac{\pi}{\mathrm{2}}}{\mathrm{2}}=−\frac{\pi}{\mathrm{4}}. \\ $$$${how}\:{get}\:\mathrm{1}−\frac{\pi}{\mathrm{4}}\:{sir}? \\ $$
Commented by jagoll last updated on 03/Feb/20
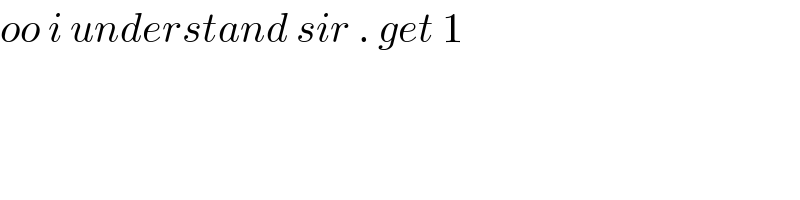
$${oo}\:{i}\:{understand}\:{sir}\:.\:{get}\:\mathrm{1}\: \\ $$
