Question Number 157096 by amin96 last updated on 19/Oct/21
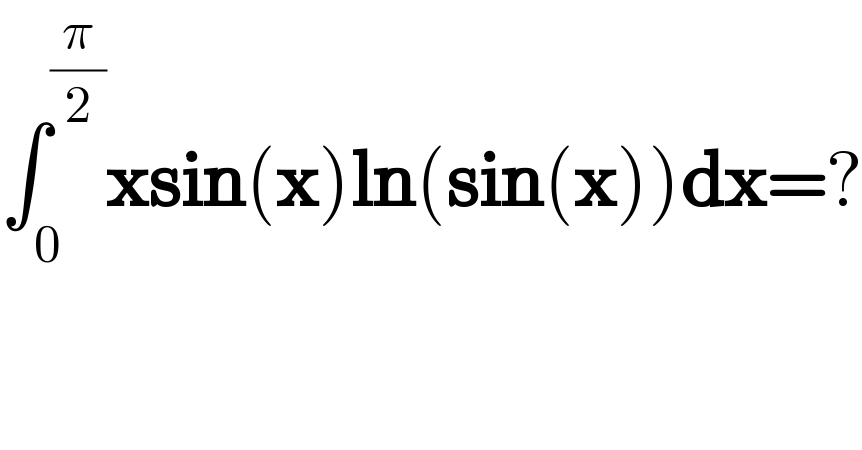
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{\mathrm{xsin}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)\right)\boldsymbol{\mathrm{dx}}=? \\ $$
Answered by mindispower last updated on 19/Oct/21
![(−xcos(x)+sin(x))ln(sin(x))]_0 ^(π/2) +∫_0 ^(π/2) ((xcos^2 (x))/(sin(x)))−cosx dx =∫_0 ^(π/2) ((x(1−sin^2 (x)))/(sin(x)))dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx−∫_0 ^(π/2) xsin(x)dx−1 =∫_0 ^(π/2) (x/(sin(x)))dx+[xcos(x)−sin(x)]_0 ^(π/2) −1 =∫_0 ^(π/2) (x/(sin(x)))dx−2,tg((x/2))=u =∫_0 ^1 ((2arctan(u))/u)du=2∫_0 ^1 Σ_(k≥0) (((−1)^k )/(2k+1))u^(2k) −2 =2Σ_(k≥0) (((−1)^k )/((2k+1)^2 ))−2=2(G−1)](https://www.tinkutara.com/question/Q157112.png)
$$\left.\left(−{xcos}\left({x}\right)+{sin}\left({x}\right)\right){ln}\left({sin}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{xcos}^{\mathrm{2}} \left({x}\right)}{{sin}\left({x}\right)}−{cosx}\:\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}\left(\mathrm{1}−{sin}^{\mathrm{2}} \left({x}\right)\right)}{{sin}\left({x}\right)}{dx}−\mathrm{1} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{{sin}\left({x}\right)}{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xsin}\left({x}\right){dx}−\mathrm{1} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{{sin}\left({x}\right)}{dx}+\left[{xcos}\left({x}\right)−{sin}\left({x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mathrm{1} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{{sin}\left({x}\right)}{dx}−\mathrm{2},{tg}\left(\frac{{x}}{\mathrm{2}}\right)={u} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{arctan}\left({u}\right)}{{u}}{du}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}{u}^{\mathrm{2}{k}} −\mathrm{2} \\ $$$$=\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{2}=\mathrm{2}\left({G}−\mathrm{1}\right) \\ $$$$ \\ $$
