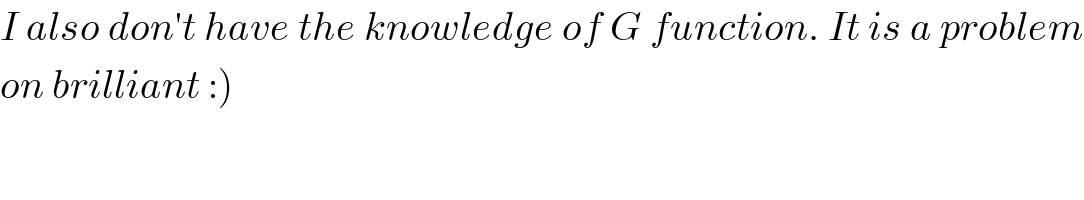0-pi-24-log-tan-d-Problem-source-brilliant-

Question Number 122013 by Dwaipayan Shikari last updated on 13/Nov/20

\int_{0}^{\frac{π}{24}} l o g (t a n θ) d θ

P r o b l e m s o u r c e : b r i l l i a n t

Commented by Dwaipayan Shikari last updated on 13/Nov/20

https://brilliant.org/problems/how-does-g-function-appears Explore the real problem on brilliant website or app

Commented by Dwaipayan Shikari last updated on 13/Nov/20

Commented by mindispower last updated on 13/Nov/20

w h a t i s G s i r

Commented by Dwaipayan Shikari last updated on 13/Nov/20

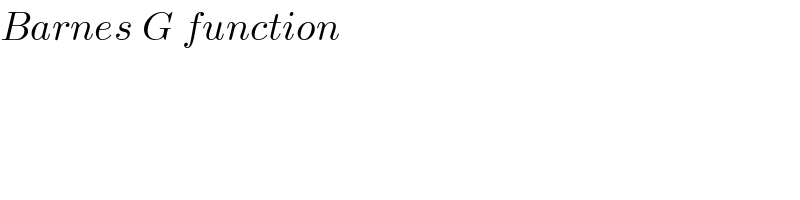
B a r n e s G f u n c t i o n

Commented by AbdullahMohammadNurusSafa last updated on 13/Nov/20

G = 6.673 \times 10^{- 11} {N m}^{2} {k g}^{- 2}

G i s a G r a v i t a t i o n a l C o n s t e n t .

Commented by Dwaipayan Shikari last updated on 14/Nov/20

I a l s o {d o n}^{'} t h a v e t h e k n o w l e d g e o f G f u n c t i o n . I t i s a p r o b l e m

o n b r i l l i a n t :)