Question Number 152730 by puissant last updated on 31/Aug/21
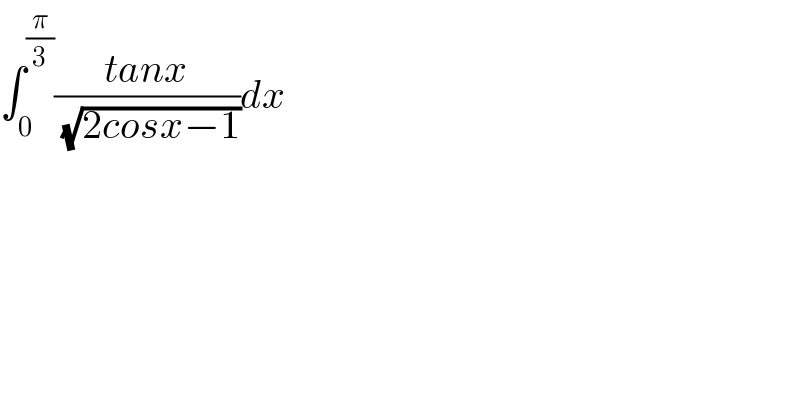
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{{tanx}}{\:\sqrt{\mathrm{2}{cosx}−\mathrm{1}}}{dx} \\ $$
Answered by Olaf_Thorendsen last updated on 31/Aug/21
![I = ∫_0 ^(π/3) ((tanx)/( (√(2cosx−1)))) Let u = cosx : I = ∫_1 ^(1/2) (((−du)/u)/( (√(2u−1)))) I = ∫_(1/2) ^1 (du/( u(√(2u−1)))) I = ∫_(1/2) ^1 (((2du)/(2(√(2u−1))))/( u)) I = 2∫_(1/2) ^1 (((2du)/(2(√(2u−1))))/( 1+((√(2u−1)))^2 )) I = 2[arctan((√(2u−1)))]_(1/2) ^1 I = 2((π/4)) = (π/2)](https://www.tinkutara.com/question/Q152732.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{tan}{x}}{\:\sqrt{\mathrm{2cos}{x}−\mathrm{1}}} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{cos}{x}\:: \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\frac{−{du}}{{u}}}{\:\sqrt{\mathrm{2}{u}−\mathrm{1}}} \\ $$$$\mathrm{I}\:=\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{du}}{\:{u}\sqrt{\mathrm{2}{u}−\mathrm{1}}} \\ $$$$\mathrm{I}\:=\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{\frac{\mathrm{2}{du}}{\mathrm{2}\sqrt{\mathrm{2}{u}−\mathrm{1}}}}{\:{u}} \\ $$$$\mathrm{I}\:=\:\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{\frac{\mathrm{2}{du}}{\mathrm{2}\sqrt{\mathrm{2}{u}−\mathrm{1}}}}{\:\mathrm{1}+\left(\sqrt{\mathrm{2}{u}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\mathrm{2}\left[\mathrm{arctan}\left(\sqrt{\mathrm{2}{u}−\mathrm{1}}\right)\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)\:=\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by Olaf_Thorendsen last updated on 31/Aug/21
![En fait on a : I = ∫_0 ^(π/3) ((tanx)/( (√(2cosx−1)))) dx I = −2∫_0 ^(π/3) (((−2sinx)/( 2(√(2cosx−1))))/( 1+((√(2cosx−1)))^2 )) dx I = −2∫_0 ^(π/3) (((d/dx)((√(2cosx−1))))/( 1+((√(2cosx−1)))^2 )) I = −2[arctan(√(2cosx−1))]_0 ^(π/3) Souvent on a le re^� sultat sous les yeux mais on ne le voit pas tout de suite.](https://www.tinkutara.com/question/Q152738.png)
$$\mathrm{En}\:\mathrm{fait}\:\mathrm{on}\:\mathrm{a}\:: \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{tan}{x}}{\:\sqrt{\mathrm{2cos}{x}−\mathrm{1}}}\:{dx} \\ $$$$\mathrm{I}\:=\:−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\frac{−\mathrm{2sin}{x}}{\:\mathrm{2}\sqrt{\mathrm{2cos}{x}−\mathrm{1}}}}{\:\mathrm{1}+\left(\sqrt{\mathrm{2cos}{x}−\mathrm{1}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{I}\:=\:−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\frac{{d}}{{dx}}\left(\sqrt{\mathrm{2cos}{x}−\mathrm{1}}\right)}{\:\mathrm{1}+\left(\sqrt{\mathrm{2cos}{x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:−\mathrm{2}\left[\mathrm{arctan}\sqrt{\mathrm{2cos}{x}−\mathrm{1}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$ \\ $$$$\mathrm{Souvent}\:\mathrm{on}\:\mathrm{a}\:\mathrm{le}\:\mathrm{r}\acute {\mathrm{e}sultat}\:\mathrm{sous}\:\mathrm{les}\:\mathrm{yeux} \\ $$$$\mathrm{mais}\:\mathrm{on}\:\mathrm{ne}\:\mathrm{le}\:\mathrm{voit}\:\mathrm{pas}\:\mathrm{tout}\:\mathrm{de}\:\mathrm{suite}. \\ $$
Commented by puissant last updated on 31/Aug/21

$${Genial}\:! \\ $$
Commented by puissant last updated on 01/Sep/21
����������������
