Question Number 165320 by mnjuly1970 last updated on 29/Jan/22
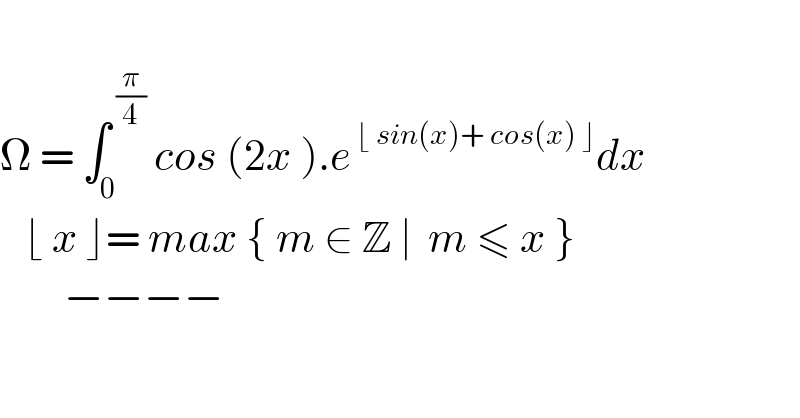
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:{cos}\:\left(\mathrm{2}{x}\:\right).{e}^{\:\lfloor\:{sin}\left({x}\right)+\:{cos}\left({x}\right)\:\rfloor} {dx} \\ $$$$\:\:\:\lfloor\:{x}\:\rfloor=\:{max}\:\left\{\:{m}\:\in\:\mathbb{Z}\:\mid\:\:{m}\:\leqslant\:{x}\:\right\} \\ $$$$\:\:\:\:\:\:\:\:−−−− \\ $$
Answered by mahdipoor last updated on 30/Jan/22
![sinx+cosx=(√2)sin((π/4)+x)=A 0≤x≤(π/4) ⇒ 1≤A≤(√2) ⇒ ⌊A⌋=1 Ω=∫_0 ^(π/4) cos(2x).e^1 .dx=e[((sin(2x))/2)]_0 ^(π/4) =(e/2)](https://www.tinkutara.com/question/Q165336.png)
$${sinx}+{cosx}=\sqrt{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)={A} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{4}}\:\Rightarrow\:\mathrm{1}\leqslant{A}\leqslant\sqrt{\mathrm{2}}\:\Rightarrow\:\lfloor{A}\rfloor=\mathrm{1} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}\left(\mathrm{2}{x}\right).{e}^{\mathrm{1}} .{dx}={e}\left[\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} =\frac{{e}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 30/Jan/22
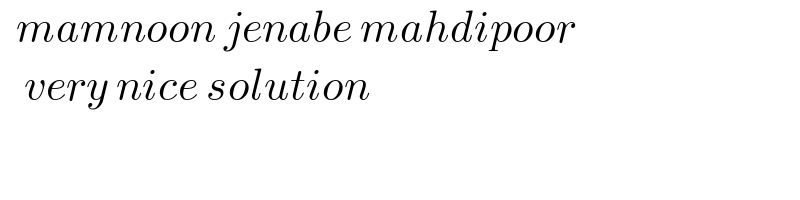
$$\:\:{mamnoon}\:{jenabe}\:{mahdipoor} \\ $$$$\:\:\:{very}\:{nice}\:{solution} \\ $$
