Question Number 151421 by peter frank last updated on 21/Aug/21
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$
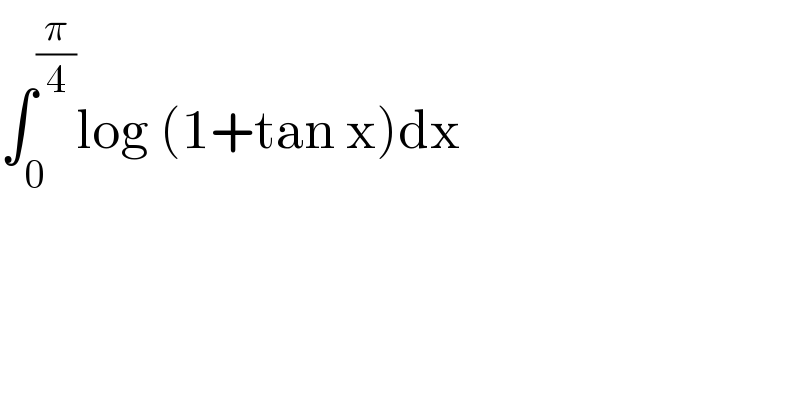
Commented by puissant last updated on 21/Aug/21
$${x}=\frac{\pi}{\mathrm{4}}−{t}\:\rightarrow\:{dx}=−{dt} \\ $$$${Q}=\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} {ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right)\left(−{dt}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tant}}{\mathrm{1}+{tant}}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{1}+{tant}}{\mathrm{1}+{tant}}+\frac{\mathrm{1}−{tant}}{\mathrm{1}+{tant}}\right){dt} \\ $$$$\Rightarrow\:{Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tant}}\right){dt} \\ $$$$\Rightarrow\:{Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tant}\right){dt} \\ $$$$\Rightarrow\:\mathrm{2}{Q}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\because\therefore\:\:{Q}=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}… \\ $$
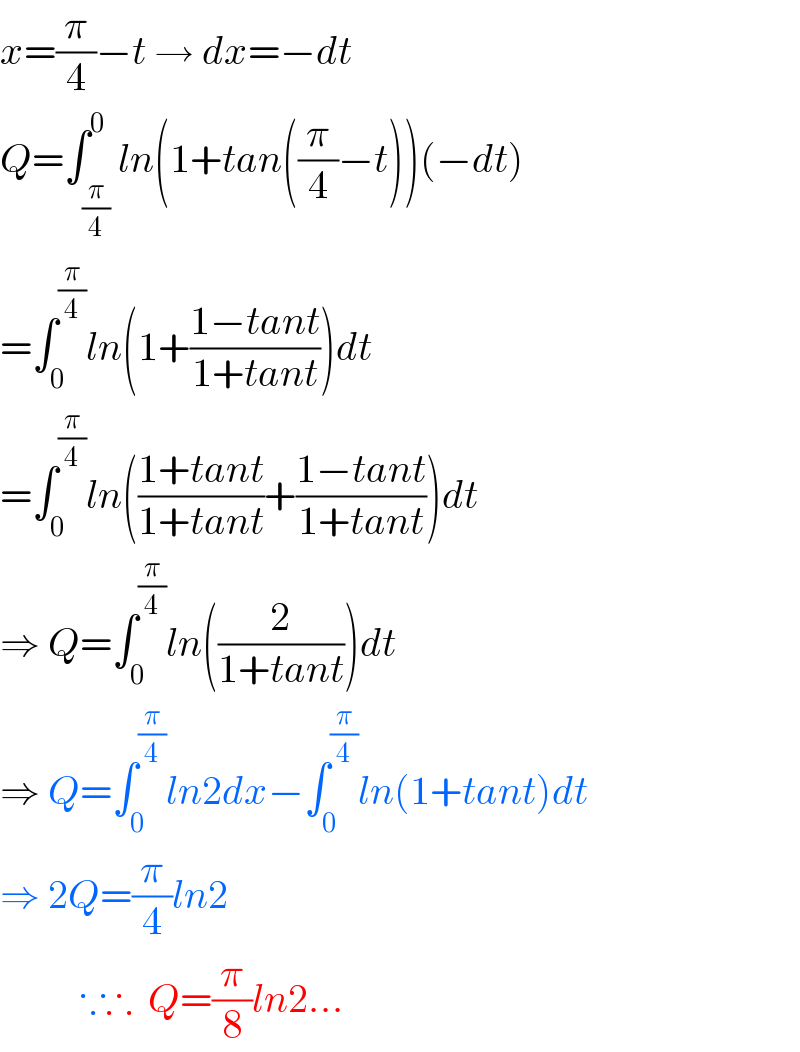
Commented by peter frank last updated on 21/Aug/21
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by peter frank last updated on 21/Aug/21
![x=(π/4)−θ dx=−dθ (0,(π/4))⇔((π/4),0) ∫_0 ^(π/4) log [1+tan ((π/4)−θ)]dθ ∫_0 ^(π/4) log [1+((tan (π/4)−tan θ)/(1+tan (π/4)tan θ))] ∫_0 ^(π/4) log[ (2/(1+tan θ))]dθ ∫_0 ^(π/4) log 2dθ−∫_0 ^(π/4) log (1+tan θ) 2I=log 2[θ]_0 ^(π/4) I=(π/8)log 2](https://www.tinkutara.com/question/Q151422.png)
$$\mathrm{x}=\frac{\pi}{\mathrm{4}}−\theta \\ $$$$\mathrm{dx}=−\mathrm{d}\theta \\ $$$$\left(\mathrm{0},\frac{\pi}{\mathrm{4}}\right)\Leftrightarrow\left(\frac{\pi}{\mathrm{4}},\mathrm{0}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\left[\mathrm{1}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right]\mathrm{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\left[\mathrm{1}+\frac{\mathrm{tan}\:\frac{\pi}{\mathrm{4}}−\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:\frac{\pi}{\mathrm{4}}\mathrm{tan}\:\theta}\right] \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\left[\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}\:\theta}\right]\mathrm{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\mathrm{2d}\theta−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\left(\mathrm{1}+\mathrm{tan}\:\theta\right) \\ $$$$\mathrm{2I}=\mathrm{log}\:\mathrm{2}\left[\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$\mathrm{I}=\frac{\pi}{\mathrm{8}}\mathrm{log}\:\mathrm{2} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 21/Aug/21
![f(a)=∫_0 ^(π/4) log(1+atanx)dx (a>0) ⇒ f^′ (a)=∫_0 ^(π/4) ((tanx)/(1+atanx))=(1/a)∫_0 ^(π/4) ((1+atanx−1)/(1+atanx))dx =(π/(4a))−(1/a)∫_0 ^(π/4) (dx/(1+atanx)) [we have ∫_0 ^(π/4) (dx/(1+atanx)) =_(tanx=t) ∫_0 ^(1 ) (dt/((1+t^2 )(1+at))) F(t)=(1/((at+1)(t^2 +1)))=(α/(at+1))+((mt+n)/(t^2 +1)) α=(1/((1/a^2 )+1))=(a^2 /(1+a^2 )) lim_(t→+∞) tF(t)=(α/a) +m ⇒m=−(α/a)=−(a/(1+a^2 )) ⇒F(t)=(a^2 /((1+a^2 )(at+1)))+((−(a/(1+a^2 ))t +n)/(t^2 +1)) F(0)=(a^2 /(1+a^2 )) +n=1 ⇒n=1−(a^2 /(1+a^2 ))=(1/(1+a^2 )) ⇒ F(t)=(a^2 /((a^2 +1)(at+1)))+((−(a/(a^2 +1))t+(1/(1+a^2 )))/(t^2 +1)) ⇒∫_0 ^1 F(t)dt=(a^2 /((a^2 +1)))∫_0 ^1 (dt/(at+1))−(1/(a^2 +1))∫_0 ^(1 ) ((at−1)/(t^2 +1))dt =(a/(a^2 +1))[ln(at+1)]_0 ^1 −(a/(2(a^2 +1)))[ln(t^2 +1)]_0 ^1 +(1/(a^2 +1))(π/4) =((aln(1+a))/(a^2 +1))−((ln2)/2)×(a/(a^2 +1)) +(π/(4(a^2 +1))) ⇒ f^′ (a)=(π/(4a))−((ln(1+a))/(a^2 +1))+((ln2)/(2(a^(2 ) +1))) −(π/(4a(a^2 +1))) f(1)=f(1)−f(0)=∫_0 ^1 f^′ (a)da=∫_0 ^(π/4) log(1+tant)dt =∫_0 ^1 (π/(4a))(1−(1/(a^2 +1)))da−∫_0 ^1 ((ln(1+a))/(a^2 +1))da+((ln2)/2)∫_0 ^1 (da/(1+a^2 )) =(π/4)∫_0 ^1 (a/(a^2 +1))da−∫_0 ^1 ((ln(1+a))/(1+a^2 ))da+(π/4)×((ln2)/2) =(π/8)[ln(a^2 +1)]_0 ^1 +((πln2)/8)−∫_0 ^1 ((ln(1+a))/(1+a^2 ))da (a=tanθ) =((πln(2))/8)+((πln2)/8)−∫_0 ^(π/4) ((ln(1+tanθ))/(1+tan^2 θ))(1+tan^2 θ)dθ =((πln2)/4)−I ⇒2I=((πln2)/4) ⇒I=(π/8)ln(2) ⇒ ∫_0 ^(π/4) ln(1+tanθ)dθ=(π/8)ln(2)](https://www.tinkutara.com/question/Q151427.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\left(\mathrm{1}+\mathrm{atanx}\right)\mathrm{dx}\:\:\:\:\:\left(\mathrm{a}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{tanx}}{\mathrm{1}+\mathrm{atanx}}=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{atanx}−\mathrm{1}}{\mathrm{1}+\mathrm{atanx}}\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4a}}−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{atanx}}\:\left[\mathrm{we}\:\mathrm{have}\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{atanx}}\:=_{\mathrm{tanx}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{at}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\left(\mathrm{at}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}=\frac{\alpha}{\mathrm{at}+\mathrm{1}}+\frac{\mathrm{mt}+\mathrm{n}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\frac{\alpha}{\mathrm{a}}\:+\mathrm{m}\:\Rightarrow\mathrm{m}=−\frac{\alpha}{\mathrm{a}}=−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{at}+\mathrm{1}\right)}+\frac{−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{t}\:+\mathrm{n}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:+\mathrm{n}=\mathrm{1}\:\Rightarrow\mathrm{n}=\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{at}+\mathrm{1}\right)}+\frac{−\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{t}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{at}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{\mathrm{at}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\left[\mathrm{ln}\left(\mathrm{at}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{a}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\left[\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{aln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{ln2}}{\mathrm{2}}×\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\pi}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi}{\mathrm{4a}}−\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}+\frac{\mathrm{ln2}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}\:} +\mathrm{1}\right)}\:−\frac{\pi}{\mathrm{4a}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{f}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}^{'} \left(\mathrm{a}\right)\mathrm{da}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\left(\mathrm{1}+\mathrm{tant}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\pi}{\mathrm{4a}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{da}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{da}+\frac{\mathrm{ln2}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{da}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{da}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{da}+\frac{\pi}{\mathrm{4}}×\frac{\mathrm{ln2}}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{8}}\left[\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\pi\mathrm{ln2}}{\mathrm{8}}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{da}\:\left(\mathrm{a}=\mathrm{tan}\theta\right) \\ $$$$=\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}+\frac{\pi\mathrm{ln2}}{\mathrm{8}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\frac{\pi\mathrm{ln2}}{\mathrm{4}}−\mathrm{I}\:\Rightarrow\mathrm{2I}=\frac{\pi\mathrm{ln2}}{\mathrm{4}}\:\Rightarrow\mathrm{I}=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)\mathrm{d}\theta=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by peter frank last updated on 21/Aug/21
$$\mathrm{thank}\:\mathrm{you} \\ $$