Question Number 127528 by bramlexs22 last updated on 30/Dec/20
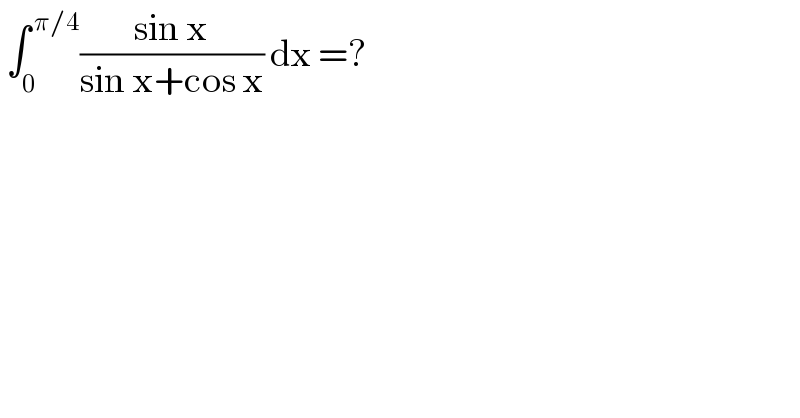
$$\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=?\: \\ $$
Answered by liberty last updated on 30/Dec/20
![Let L = ∫_0 ^( π/4) ((sin x)/(sin x+cos x)) dx and let Y = ∫_0 ^( π/4) ((cos x)/(sin x+cos x))dx (1) L+Y = ∫_0 ^( π/4) ((sin x+cos x)/(sin x+cos x)) dx = (π/4) (2) L−Y = ∫_0 ^( π/4) ((sin x−cos x)/(sin x+cos x)) dx = −∫_0 ^( π/4) ((d(sin x+cos x))/(sin x+cos x)) =−[ ln (sin x+cos x) ]_0 ^(π/4) = −(1/2)ln (2) (3) L = (((L+Y)+(L−Y))/2) = (π/8)−(1/4)ln (2)](https://www.tinkutara.com/question/Q127530.png)
$$\:{Let}\:{L}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\: \\ $$$$\:{and}\:{let}\:{Y}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx} \\ $$$$\left(\mathrm{1}\right)\:{L}+{Y}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:{L}−{Y}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \frac{{d}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\left[\:\mathrm{ln}\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)\:\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{3}\right)\:{L}\:=\:\frac{\left({L}+{Y}\right)+\left({L}−{Y}\right)}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 30/Dec/20

$$\mathrm{amazing}… \\ $$
Answered by Dwaipayan Shikari last updated on 30/Dec/20
![∫_0 ^1 (t/(t+1)).(1/(t^2 +1))dt tanx=t =(1/2)∫_0 ^1 t((1/(t+1))−((t−1)/(t^2 +1)))dt =(1/2)∫_0 ^1 −(1/(t+1))+(t/(t^2 +1))+(1/(1+t^2 ))dt=[(1/2)log(((√(t^2 +1))/(t+1)))]_0 ^1 +[(1/2)tan^(−1) t]_0 ^1 =(π/8)−(1/4)log(2)](https://www.tinkutara.com/question/Q127535.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}}{{t}+\mathrm{1}}.\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tanx}={t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}\left(\frac{\mathrm{1}}{{t}+\mathrm{1}}−\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\left[\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}+\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {t}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}{log}\left(\mathrm{2}\right) \\ $$
Answered by mathmax by abdo last updated on 31/Dec/20
![I=∫_0 ^(π/4) ((sinx)/(sinx +cosx))dx we do the changement tan((x/2))=t ⇒ I =∫_0 ^((√2)−1) (((2t)/(1+t^2 ))/(((2t)/(1+t^2 )) +((1−t^2 )/(1+t^2 ))))×((2dt)/(1+t^2 )) =∫_0 ^((√2)−1) ((4t)/((1+t^2 )(−t^2 +2t+1)))dt =−4 ∫_0 ^((√2)−1) ((tdt)/((t^2 +1)(t^2 −2t−1))) let decompose F(t)=(t/((t^2 +1)(t^2 −2t−1))) t^2 −2t−1=0 →Δ^′ =1+1=2 ⇒t_1 =1+(√2) and t_2 =1−(√2) F(t)=(a/(t−t_1 ))+(b/(t−t_2 )) +((ct +d)/(t^2 +1)) a=(t_1 /((t_1 ^2 +1)(t_1 −t_2 ))) =((1+(√2))/(2(√2)(1+3+2(√2)))) =((1+(√2))/(2(√2)(4+2(√2)))) b=(t_2 /((t_2 ^2 +1)(t_2 −t_1 ))) =((1−(√2))/((−2(√2))(3−2(√2))+1)))=(((√2)−1)/(2(√2)(4−2(√2)))) lim_(t→+∞) tF(t)=0 =a+b +c ⇒c=−a−b F(0)=0 =−(a/t_1 )−(b/t_2 ) +d ⇒d=(a/t_1 )+(b/t_2 ) ⇒ ∫_0 ^((√2)−1) F(t)dt =a∫_0 ^((√2)−1) (dt/(t−t_1 ))+b ∫_0 ^((√2)−1) (dt/(t−t_2 )) +(c/2)∫_0 ^((√2)−1) ((2t)/(t^2 +1))dt +d ∫_0 ^((√2)−1) (dt/(t^2 +1)) =a[ln∣t−t_1 ∣]_0 ^((√2)−1) +b[ln∣t−t_2 ∣]_0 ^((√2)−1) +(c/2)[ln(t^2 +1)]_0 ^((√2)−1) +d [arctant]_0 ^((√2)−1) rest to finish calculus...](https://www.tinkutara.com/question/Q127585.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sinx}}{\mathrm{sinx}\:+\mathrm{cosx}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{4t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(−\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{tdt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2t}−\mathrm{1}\right)}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2t}−\mathrm{1}\right)} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{2t}−\mathrm{1}=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}+\mathrm{1}=\mathrm{2}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\:+\frac{\mathrm{ct}\:+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}=\frac{\mathrm{t}_{\mathrm{1}} }{\left(\mathrm{t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}_{\mathrm{1}} −\mathrm{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}+\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{b}=\frac{\mathrm{t}_{\mathrm{2}} }{\left(\mathrm{t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}_{\mathrm{2}} −\mathrm{t}_{\mathrm{1}} \right)}\:=\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\left.\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)+\mathrm{1}\right)}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \:\mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:+\mathrm{c}\:\Rightarrow\mathrm{c}=−\mathrm{a}−\mathrm{b} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\mathrm{0}\:=−\frac{\mathrm{a}}{\mathrm{t}_{\mathrm{1}} }−\frac{\mathrm{b}}{\mathrm{t}_{\mathrm{2}} }\:+\mathrm{d}\:\Rightarrow\mathrm{d}=\frac{\mathrm{a}}{\mathrm{t}_{\mathrm{1}} }+\frac{\mathrm{b}}{\mathrm{t}_{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{a}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }+\mathrm{b}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$+\mathrm{d}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{a}\left[\mathrm{ln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{1}} \mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\mathrm{b}\left[\mathrm{ln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\frac{\mathrm{c}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$+\mathrm{d}\:\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{calculus}… \\ $$
